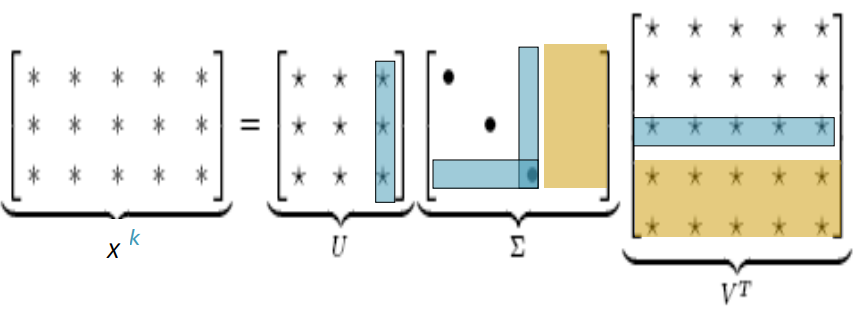
○ Full singular value decomposition(SVD)
Reference)
SVD와 PCA, 그리고 잠재의미분석(LSA)
Singular Value Decomposition Tutorial
직사각형 행렬 $A$는 직교성 행렬 $U$와 대각행렬 $S$그리고 직교성 행렬의 전치행렬인 $V$로 분해된다.
$A_{mn}=U_{mm}S_{mn}V_{nn}^T$
이 때 $U^{T}U=I$, $V^{T}V=I$일 때, $U$는 $AA^{T}$의 직교성 eigenvectors($m,m$ 차원), $V$는 $A^{T}A$의 직교성 eigenvecter($n,n$ 차원) $S$는 $U$또는 $V$의 eigenvalue의 제곱근을 대각행렬로 갖는다.
예시를 들어보자 $A$가 하기와 같을 때
$A = \begin{bmatrix}
3 & 1 & 1 \\
-1 & 3 & 1 \\
\end{bmatrix}$
$U$를 찾기 위해서 우리는 $AA^{T}$를 구해야하므로,
$A^{T} = \begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1 \\
\end{bmatrix}$
그러므로,
$AA^{T} = \begin{bmatrix} 3 & 1 & 1 \\ -1 & 3 & 1 \\ \end{bmatrix}\begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 11 & 1 \\ 11 & 1 \\ \end{bmatrix}$
다음, 우리는 $AA^{T}$에 해당하는 eigenvalues 와 eigenvectors를 찾아야합니다. 이는 $AA^{T}\vec{\upsilon }=\lambda\vec{\upsilon }$으로 표현되므로,
$\begin{bmatrix}
11 & 1 \\
1 & 11 \\
\end{bmatrix}\begin{bmatrix}
x_{1} \\
x_{2} \\
\end{bmatrix}=\lambda I\begin{bmatrix}
x_{1} \\
x_{2} \\
\end{bmatrix}$
좌변으로 정리하면,
$\begin{bmatrix}
11 - \lambda & 1 \\
1 & 11 - \lambda \\
\end{bmatrix}\begin{bmatrix}
x_{1} \\
x_{2} \\
\end{bmatrix}=0$
이 때, eigenvector가 0이 아니므로 좌항의 역행렬이 존재하면 안된다. 따라서 $det(좌항)=0$,
$\begin{vmatrix}
11-\lambda & 1 \\
1 & 11-\lambda \\
\end{vmatrix}=0$
$(11-\lambda)(11-\lambda)-1 \cdot 1=0$
$(\lambda-10)(\lambda-12)=0$
$\therefore \lambda=10, \lambda=12$
이제 $\lambda$를 원래 식에 대입하면 $\lambda=10$일 때,
$(11-10)x_{1} + x_{2}=0, \: \therefore x_{1} = -x_{2}$
다양한 값들이 가능하지만 작고 쉬운 값인 $x_{1}=1$과 $x_{2}=-1$ 를 취하면 eigenvector는 $\begin{bmatrix}
1 & -1 \\
\end{bmatrix} $가 된다.
또한 $\lambda=12$일 때,
$(11-12)x_{1} + x_{2}=0, \: \therefore x_{1} = x_{2}$
같은 이유로 $x_{1}=1$과 $x_{2}=1$ 를 취하면 eigenvector는 $\begin{bmatrix}
1 & 1 \\
\end{bmatrix} $가 된다.
이제 eigenvalue($\lambda$)의 내림차순으로 eigenvector가 열에 나열된다.
$\lambda = 12 \rightarrow \begin{bmatrix}
1 & 1 \\
1 & -1 \\
\end{bmatrix} \leftarrow \lambda = 10$
이후 eigenvalue가 가장 큰 첫번째 열을 기준으로 Gram-Schmidt orthonormalization process를 진행한다.
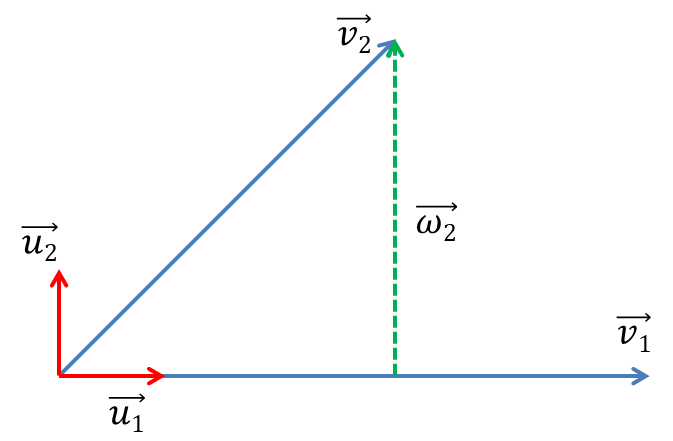
1열인 $\vec{v_{1}}$의 normalize를 수행하면
$\vec{u_{1}} = \frac{\vec{v_{1}}}{\vec{v_{1}}} = \frac{[1,1]}{\sqrt{1^{2}+1^{2}}} = \frac{[1,1]}{\sqrt{2}}=\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix}$
이 후 $\vec{\omega_{2}}=\vec{v_{2}}-\vec{u_{1}}\cdot\vec{v_{2}}\ast \vec{u_{1}}$ 에 대입하여
$\begin{bmatrix}
1 & -1 \\
\end{bmatrix}-\begin{bmatrix}
1/\sqrt{2} & 1/\sqrt{2} \\
\end{bmatrix}\cdot\begin{bmatrix}
1 & -1 \\
\end{bmatrix}\ast \begin{bmatrix}
1/\sqrt{2} & 1/\sqrt{2} \\
\end{bmatrix}$
$\begin{bmatrix}
1 & -1 \\
\end{bmatrix}-0\ast \begin{bmatrix}
1/\sqrt{2} & 1/\sqrt{2} \\
\end{bmatrix}=\begin{bmatrix}
1 & -1 \\
\end{bmatrix}-\begin{bmatrix}
0 & 0 \\
\end{bmatrix} = \begin{bmatrix}
1 & -1 \\
\end{bmatrix}$
이후 normalize
$\vec{u_{2}}=\frac{\vec{\omega_{2}}}{|\vec{\omega_{2}}|} = \begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix}$
$$\therefore U=\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix}$$
같은 방식으로 $V$에 대해서도 $A^{T}A$를 기반으로 진행하면 다음과 같이 된다. (상세 수식은 reference 참고)
$V=\begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{30}} \\
\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{30}} \\
\frac{1}{\sqrt{6}} & 0 & -\frac{5}{\sqrt{30}} \\
\end{bmatrix}$
$V^{T}=\begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\
\frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{5}} & 0 \\
\frac{1}{\sqrt{30}} & \frac{2}{\sqrt{30}} & -\frac{5}{\sqrt{30}} \\
\end{bmatrix}$
$S$의 경우는 0이 아닌 eigenvalues에 대해 제곱근을 씌워서 내림차순으로 $U$의 차원인 $m$만큼 대각행렬을 구성하면 된다. 0이 아닌 $U$와 $V$의 eigenvalues는 항상 수가 같다. 따라서 어느 eigenvalues를 사용하는가는 문제가 되지 않는다. 따라서 차원을 일치시키기 위해 $m-n$만큼 0 열을 추가해주어야한다.
$S = \begin{bmatrix}
\sqrt{12} & 0 & 0 \\
0 & \sqrt{10} & 0 \\
\end{bmatrix}$
따라서 직각 행렬 $A$는 다음과 같이 분해된다
$A_{mn}=U_{mm}S_{mn}V_{nn}^{T} = \begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix} \begin{bmatrix}
\sqrt{12} & 0 & 0 \\
0 & \sqrt{10} & 0 \\
\end{bmatrix} \begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\
\frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{5}} & 0 \\
\frac{1}{\sqrt{30}} & \frac{2}{\sqrt{30}} & -\frac{5}{\sqrt{30}} \\
\end{bmatrix}$
$A_{mn}=U_{mm}S_{mn}V_{nn}^{T} = \begin{bmatrix}
\frac{\sqrt{12}}{\sqrt{2}}& \frac{\sqrt{10}}{\sqrt{2}} & 0 \\
\frac{\sqrt{12}}{\sqrt{2}} & -\frac{\sqrt{10}}{\sqrt{2}} & 0 \\
\end{bmatrix} \begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\
\frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{5}} & 0 \\
\frac{1}{\sqrt{30}} & \frac{2}{\sqrt{30}} & -\frac{5}{\sqrt{30}} \\
\end{bmatrix}=\begin{bmatrix}
3 & 1 & 1 \\
-1 & 3 & 1 \\
\end{bmatrix}$
이후 기준으로 잡고자하는 차원($n$ 또는 $m$)에 보고자하는 eigenvalue의 수만큼 $U^{T}$나 $V$를 차원을 축소한 후 내적하여 해당 eigenvector를 기준으로 맞추어서 데이터를 사용한다.
○ Reduced Singular Value Decomposition
문헌 추출과 단어 유사도 비교 등 Latent Semantic Indexing or Latent Semantic Analysis라고 불리는 수학 기법이다. 일반적으로 단어 x 문서 행렬을 선형 독립 구성 요소로 분해하여 기저의 핵심만 사용한다. 이를 통해 노이즈가 많은 상관 관계에서 각 차원을 따라 데이터의 기본 구조에 가장 근접하는 값의 집합만 추출된다. 이 요소들은 매우 작기 때문에 결과적으로 작은 원본보다 훨씬 적은 차원으로 원본을 기술한다. 이러한 차원 감소는 유사한 하부구조는 더 유사해지고 다른 하부구조는 더욱 달라지는 이점이 있다. 예를 들어 특정 주제의 문서들 간 같은 단어가 등장하지 않더라도 서로 유사해진다.