1-2) Elementary of mathmatics

출처: https://www.edwith.org/bayesiandeeplearning/lecture/24678?isDesc=false

Probability

학습 목표

Set이 정의되어 있어야 그 위에 Measure를 정의할 수 있고,
Measure가 있어야 Probability를 정의할 수 있습니다.
그래서 이전 학습을 통해 Set과 Measure에 대해서 공부해보았습니다.
이제부터는 베이지안 딥러닝을 공부하기에 앞서 꼭 필요한 개념인 Probability에 대해서 구체적으로 공부해보도록 합시다. 

Keywords

• 확률(Probability)
• 표본공간(Sample space)
• 확률 시행(Random experiment)
• 확률 질량 함수(Probability mass function)
• 베이즈정리(Bayes' theorem)
• 기댓값(Expectation)

Toss a fair dice and observe the outcomes. 모든 가능한 경우의 수를 고려야해하므로 $\sigma$-field를 power set이라고 정의하자. 여기서 $\Omega$는 sample space이다.

여기서 각각의 눈이 나올 확률은 sample space에서 정의된 면적과 같다.

$$P(\left \{ 1\right \} ) = P(\left \{ 2\right \} ) = P(\left \{ 3\right \} ) = P(\left \{ 4\right \} ) = P(\left \{ 5\right \} ) = P(\left \{ 6\right \} ) = 1/6$$
$$P(A) = P(2, 4, 6) = P(\left \{ 2\right \} ) + P(\left \{ 4\right \} ) + P(\left \{ 6\right \} ) = 1/2$$

 

• The random experiment should be well defined.
• The outcomes are all the possible results of the random experiment each of which canot be further divided. (outcome $\neq$ sample space)
• The sample point $w$: a point representing an outcome.
• The sample space $\Omega$
  : the set of all the sample points.
• Definition (probability)
  • $P$ defined on a measurable space $(\Omega, \mathcal{A})$ is a set function 
    $P$ : $\mathcal{A} \rightarrow [0, 1]$ such that (probability axioms). ($A$는 $\sigma$-field 이며, 0에서 1사이로 measure되고)
    1. $P(\varnothing )=0$ (empty set은 0)
    2. $P(A) \geq  0 \forall A \subseteq \Omega$ (항상 0이상이고)
    3. For disjoint sets $A_i$ and $A_j \Rightarrow P(\cup^k_{i=1}A_i)=\sum_{i=1}^{k}P(A_i)$ (countable additivity, disjoint set에 대해서 더하면 더해지는)
    4. $P(\Omega)=1$ (normalize 되었기 때문에 set 전체가 들어가면 1)
• probability allocation function
  
  • For discrete $\Omega$: (probability mass function)
    $p:\Omega \rightarrow [0,1]$ such that $\sum_{w\in \Omega}p(w)=1$ and $P(A)=\sum_{w\in A}p(w)$
  • For continuous $\Omega$: (probability distribution function)
    $f:\Omega \rightarrow [0, \infty)$ such that $\int_{w\in \Omega}f(w)dw=1$ and $P(A)=\int_{w\in \Omega}f(w)dw$.
  • Recall that probability $P$ is a set function $P : A \rightarrow [0; 1]$ where $A$ is a $\sigma$-field.
    :결국 sample space에서 확률의 정의를 만족하는 함수들을 찾다보니 gaussian distribution 같은 분포가 나온 것

Examples of probability allocation function. Sample space ($\Omega)위에 정의된 것을 확인할 수 있다. 또한 검은색 Bold line은$\sigma$-field 이며, 이를 통해 probability가 정의되는 것을 알 수 있다. 해당 값은 아직 measure된 것이 아니며 probability space 안에서만 정의된 값이다.

• conditional probability of A given B:
  $$P(A|B)\overset{\underset{\mathrm{def}}{}}{=}\frac{P(A\cap B)}{P(B)}$$
• Again, recall that probability P is a set function, i.e., $P : A \rightarrow [0; 1]$.

Sample space($\Omega$) 안에 $sigma$-field 인 A 와 B의 교집합은 역시 $sigma$-field이고 따라서 확률을 면적을 통해 정의할 수 있다.

• From the definition of conditional probability, we can derive:
• chain rule:
  $P(A \cap B) = P(A|B)P(B)$
  $P(A \cap B \cap C) = P(A|B \cap C)P(B \cap C) = P(A|B \cap C)P(B|C)P(C)$
• total probability law:
  $P(A) = P(A \cap B) + P(A \cap B^C ) \\= P(A|B)P(B) + P(A|B^C )P(B^C )$
• Bayes' rule
  $p(B|A)=\frac{P(B\cap A)}{P(A)}=\frac{P(A\cap B)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$
• When B(로또를 맞을 확률) is the event that is considered and A(전날 밤에 꾼 꿈) is an observation,
  • $P(B|A)$ is called posterior probability.
  • $P(B)$ is called prior probability.
• independent events $A$ and $B$: $P(A \cap B) = P(A)P(B)$

즉 정의에 따라 교집합이 없는게 independent가 아니다

• independent $\neq$ disjoint, mutually exclusive

independent 한 예시

Random variable

학습 목표

이전 수업을 통해서 확률에 대해서 공부하면서, 확률 공간에 대해서 정의하였습니다.

확률 공간에서는 확률적인 과정에 따라 값이 결정되는 변수가 있는데

그 변수를 확률 변수(Random variable)이라고 부릅니다.

이번 시간에는 확률 변수에 대해서 공부해보도록 해요.

Keywords

• 확률변수(Random variable)
• 확률공간(Probability space)
• 확률 밀도 함수(Probability density function)
• 상관분석(Correlation analysis)

 

• random variable:
  A random variable is a real-valued function defined on $\Omega$ that is measurable w.r.t. the probability space $(\Omega,A,P)$ and the Borel measurable space $(\mathbb{R}, \mathcal{B})$, i.e.,
  $X : \Omega \rightarrow \mathbb{R}$ such that $\forall B \in \mathcal{B}, X^{-1}(B)\in A.$
  :sample space에서 하나의 원소가 특정 실수에 대응되는 함수, 확률은 sample space $\sigma$-field 에서 정의된 set function
  :여기서 inverse image(역함수)로 표시한 것은 주사위의 1과 2가 나올 확률을 구하기 위해 1과 2가 차지하는 면적을 구하기 위해 원래 sample space에서 만들어지는 $\sigma$-field 안에 들어가게하고 싶은 것
  *Borel set: 실수들의 집합($\mathbb{R}$)으로 만들어지는 $\sigma$-field 
  
  • What is random here?
    : sample space에서 하나를 뽑는 것, 함수이기 때문에 그에 해당하는 값이 튀어나옴
  • What is the result of carrying out the random experiment?
    : 결과는 관측치가 하나 나오는 것

• Random variables are real numbers of our interest that are associated with the outcomes of a random experiment.
• $X(w)$ for a specific $w\in \Omega$ is called a realization. (즉, sampling이 realization)
• The set of all realizations of $X$ is called the alphabet of $X$. (주사위를 던질 때 alphabet은 1~6)
• We are interested in $P(X \in B)$ for $B \in \mathcal{B}$:
  $P(X \in B) \overset{\underset{\mathrm{def}}{}}{=} P(X^{-1}(B)) = P(\left \{w : X(w) \in B \right \})$
  :역함수가 차지하는 면적을 계산하는 것이 확률
• discrete random variable: There is a discrete set
  $\left\{ x_i:i=1,2,...\right\}$ such that $\sum P(X=x_i)=1$ (X라는 random variable이 x_i 값이 나올 면적의 크기)
• probability mass function: $p_X(x) \overset{\underset{\mathrm{def}}{}}{=}P(X = x)$ that satisfies
  
  1. $0\leq p_X(x) \leq 1$
  2. $\sum_x p_X(x)=1
  3. $P(X\in B) = \sum_{x\in B}p_X(x)$
• example: three fair-coin tosses
  • $X$ = number of heads
  • probability mass function (pmf)
    $$p_X(x)\left\{\begin{matrix} 1/8, & x=0 \\ 3/8, & x=1 \\ 3/8, & x=2 \\ 1/8, & x=3 \\ 0, & \texttt{else} \\ \end{matrix}\right.$$
  • $P(X\geq 1)=\frac{3}{8}+\frac{3}{8}+\frac{1}{8}=\frac{7}{8}$

probability mass function 예시, x가 distribution을 따를 때 k가 나올 확률

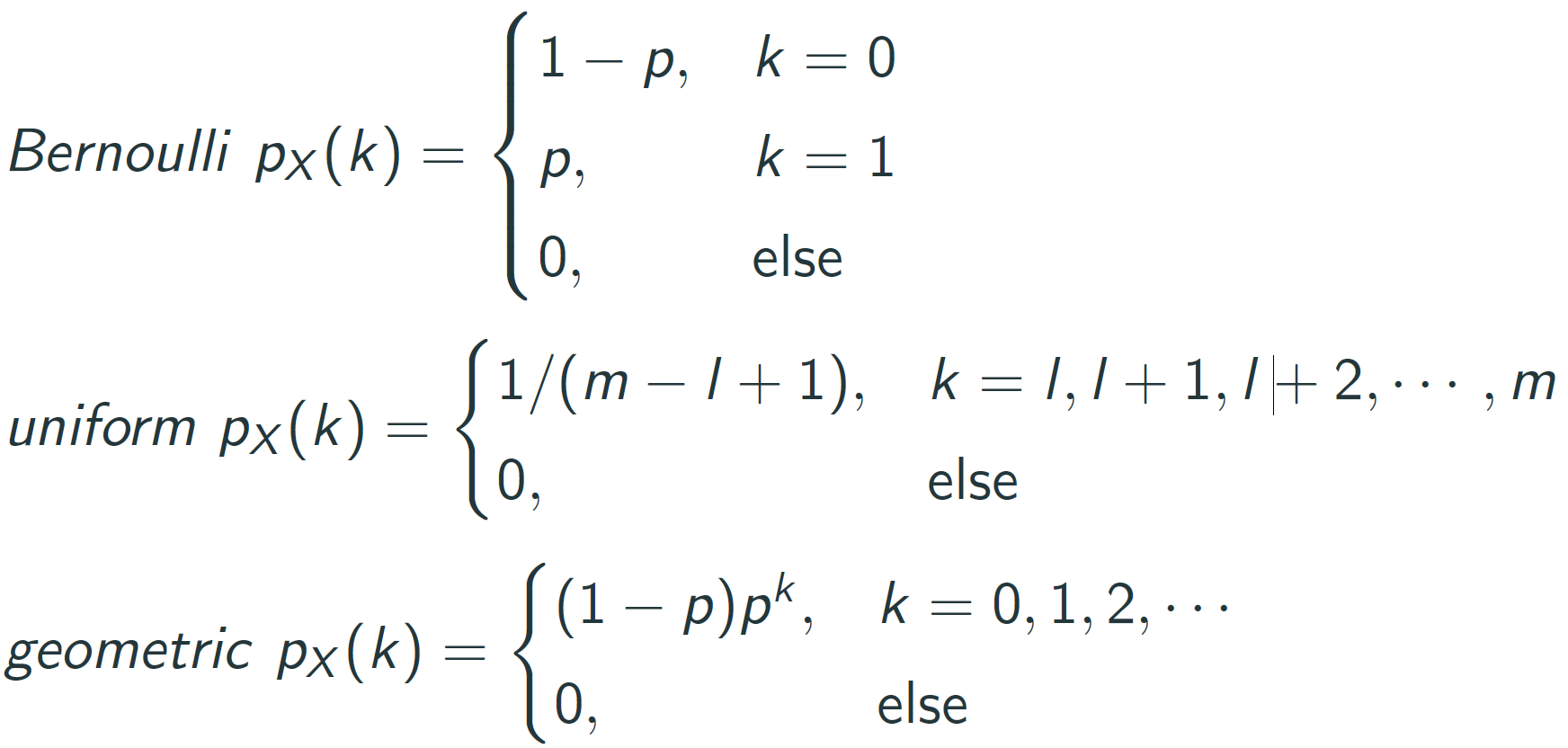
• continuous random variable
  There is an integrable function $f_X (x)$ such that
  $P(X\in B) =\int _{B}f_X(x)dx$
• probability density function
  $f_X(x)\overset{\underset{\mathrm{def}}{}}{=}\texttt{lim}_{\Delta x\rightarrow 0}\frac{P(x< X\leq x+\Delta x)}{\Delta x}$ that satisfies
  :pmf와 다른점은 단일 값의 확률은 면적이 0이기 때문에 0이다
  
  1. $f_X(x) > 1$ is possible
  2. $\int_{\infty }^{-\infty } f_X(x)dx=1$
  3. $P(X\in B)=\int_{x\in B}f_X(x)dx$

probability density function 예시

$$EX\overset{\underset{\mathrm{def}}{}}{=}\left\{\begin{matrix} \sum_x xp_X(x), & \texttt{discrete}X \\ \int_{\infty}^{\infty}xf_X(x)dx, & \texttt{continuous}X \\ \end{matrix}\right.$$

• Conditional expectation $E(X|Y)$ (mean 0 gaussian의 expectation 은 0이다. 즉, random variable의 expectation은 radom variable이 아니라 그 평균이다. 그러나 다른 random variable (Y)에 contional하게 되면 그 expectation ($E(X|Y)$)는 random variable이 된다.)
  • Expectation $E(X)$ of random variable $X$ is $EX=\int xf_X(x)dx$ and is a deterministic variable.
  • $E(X|Y)$ is a function of $Y$ and hence a random variable.
  • For each $y$, $E(X|Y)$ is $X$ average over the event where $Y = y$.

몸무게가 50, 60, 70, 80 kg인 사람들의 평균 키라고 생각하면 된다. 이 때 키는 연속적인 값을 가지지만 conditional expectation은 몸무게로 제한된 sample space에서 4개의 값만 가진다

• Definition (conditional expectation)
  • Given a random variable $Y$ with $\mathbb{E}|Y| < \infty$ defined on a probability space $(\Omega,A,\mathbb{P})$ and some sub-$\sigma$-field $\mathcal{G} \subset \mathcal{A}$ we will define the conditional expectation as the almost surely unique random variable $\mathbb{E}(Y|\mathcal{G})$ which satisfies the following two conditions
    1. $(Y|\mathcal{G})$ is $\mathcal{G}$-measurable.
    2. $\mathbb{E}(YZ) = \mathbb{E}(\mathbb{E}(Y|\mathcal{G}Z))$ for all $Z$ which are bounded and $\mathcal{G}$-measurable.
  • Conditional expectation $E(X|Y)$ with different $\sigma$-fields.

즉 condition Y를 더 자잘하게 나눌수 있다면 더 세밀하게 X의 기대값을 얻을 수 있고 이것이 resolution이 된다.

• Moment
  
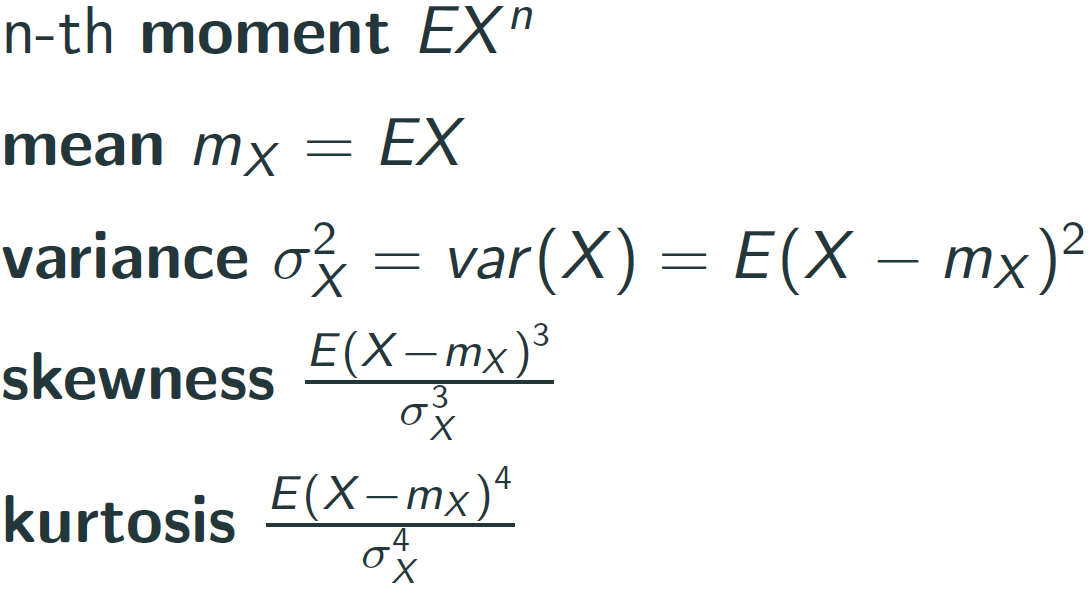
  평균은 분포를 고려하지 않기 때문에 다른 분포를 의미하는 다른 수치들과 함께 봐야한다.
• Joint Moment