1-1) Elementary of mathmatics

 

출처: https://www.edwith.org/bayesiandeeplearning/lecture/24678?isDesc=false

Introduction

학습 목표

이번 챕터에서는 Elementary of mathematics에 대해서 소개할 예정입니다.

베이지안 딥러닝에 대해서 구체적으로 공부하기 이전에 확률에 대해서 구체적으로 정의하고,

앞으로 자주보게 될 여러 용어에 대해서 정확하게 이해할 수 있도록 학습하려고 합니다.

본격적으로 학습하기에 앞서 어떤 내용을 배우게 될 지 간략하게 살펴보도록 해요.

 

Keywords

• Set theory
• Measure theory
• Probability
• Random variable
• Random process
• Functional analysis 

Whats Wrong with Probability Notation?

• Whats Wrong?
  1. overloading $p()$ for every probability function.
  2. using bound variables named after random variables.
     → 주사위의 경우, bound variables: x,y(1~6), random variable: 관측값(X,Y)
• Probability Notation is Bad
  $p(x|y) = p(y|x)p(x)=p(y)$
• Random variables don't help.
  $P_{X|Y}(x|y) = P_{Y|X}(y|x)p_X(x)=p_Y(y)$
  → 각각의 확률이 어떤 분포를 따르는지 알아야한다(gaussian, binomial, ...)
• Expectations
  $\mathbb{E}[x]=\sum_{x}{xp(x)}$
  $\mathbb{E}[X]=\sum_{x}{xP(x)}$

Today, I will introduce

1. probability theory of Kolmogorov
   • set theory
   • measure theory.
2. basic functional analysis

Andrey Kolmogorov

Import questions to have in mind throughout this lecture:

1. What is probability?
2. What is a random variable?
3. What is a random process?
4. What is a kernel function?

Set theory

학습목표
베이지안 딥러닝에 대해서 공부하기 위해서는 확률에 대해서 이해하고 있어야 합니다. 
확률이 나오게 된 배경을 이해하기 위해 Set theory와 Measure theory에 대해서 공부해야하는데,
이번에는 그 중에서 Set theory를 공부해볼거예요.
Set과 Element에 대해서 이해하고 특징들을 살펴보면서 다음 강의를 위한 기초를 다져봅시다.

핵심 키워드

• 집합론(Set theory) 
• 집합(Set)
• 집합의 원소(Element)
• 집합의 크기(Cardinality)
• 가산 집합(Countable)
• 함수(Function) / 맵핑(Mapping)

 

Set 용어(1)

• set(옷장 안의 옷들), element(옷), subset(옷의 일부), universal set(전체 옷), set operations(옷의 갯수)
• disjoint sets: $A\cap B=\varnothing $ (청바지와 코트는 겹치는게 없다)
• partition of $A$ (disjoint set으로 나누어서 전체 set이 되게 하는 것)
  example: $A = \left \{ 1,2,3,4 \right \}$, partition of A: $\left\{ \left\{1, 2 \right\}, \left\{ 3 \right\}, \left\{ 4 \right\}\right\}$
• Cartesian product: $A\times B = \left\{ (a, b):a\in A, b\in B\right\}$ (두 개의 set에서 각각 하나씩 element를 가져옴)
  example: $A=\left\{ 1,2\right\}, B=\left\{ 3,4,5 \right\}$
  $A\times B=\left\{ (1,3), (1,4), (1,5), (2,3), (2,4), (2,5)\right\}$
• power set $2^A$: the set of all the subsets of $A$. 
  example: $A=\left\{ 1, 2, 3\right\}$
  $2^A=\left\{ \varnothing ,\left\{ 1\right\},\left\{ 2\right\}, \left\{ 3\right\}, \left\{ 1,2\right\}, \left\{ 2,3\right\}, \left\{ 1,3\right\}, \left\{ 1,2,3\right\}\right\}$
• cardinality $|A|$: finite, infinite, countable, uncountable, denumerable(countably infinite) (집합 개념을 무한대로 확장하기 위해 필요)
  • $|A| = m; |B| = n \Rightarrow  |A\times B| = mn$
  • $|A|=n \Rightarrow |2^A|=2^n$
  • If there exists a one-to-one correspondence between two sets, they have the same cardinality. (Real 차원 두 개가 되면 2차원, 같은 무한대여도 cardinality가 다를 수 있다. 예를들어 정수와 실수)
  • countable: There is a one-to-one between the set and a set of natural numbers. (example: set of all integers(정수), set of all rational numbers(유리수))

Are the set of all integers and the set of all rational numbers countable?

→Yes. by the following mappings. 

위의 경우는 자연수와 정수의 관계이지만 유리수도 순서를 매길 수 있기 때문에 countable하다. 결과적으로 둘의 cardinality는 같다.

 

• denumerable: countably infinite (셀 수있는 무한대의 경우)
  All denumerable sets are of the same cardinality, which is denoted by $ℵ_0$, aleph null or aleph naught. (자연수의 개수)
• uncountable: not countable 
  The smallest known uncountable set is $(0, 1)$ or $\mathbb{R}$, the set of all real numbers, whose cardinality is denoted by $c$, continuum. $c = 2^{ℵ_0}$
  0과 1사이에 있는 실수의 개수는 몇 개인가? 크기는 정수와 같은가?

Cardinality of $C = [0, 1]$ 실수의 집합이 uncountable임을 증명하라(Cantor’s diagonal argument)

이진법에서  비가산 집합 의 존재성을 증명하는 Cantor’s diagonal argument을 나타낸 것이다. 아래에 있는 수는 위의 어느 수와도 같을 수 없다.

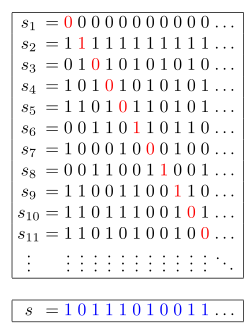
1. Suppose that C is countable.
2. Then, there exists a sequence $S = {x_1, x_2, . . .}$ such that all elements in $C$ are covered.
3. We can represent each $x_i$ using a binary system.
   $x_1 = 0.d_{11}d_{12}d_{13}... $
   $x_2 = 0.d_{21}d_{22}d_{23}... $
   $x_3 = 0.d_{31}d_{32}d_{33}... $
   where $d_{ij} \in \left \{0, 1 \right \}$.
4. Define $x_{\texttt{new}} = 0.d_1d_2d_3$ . . . such that $d_i = 1 − d_{ii}$.
5. Clearly, $x_{new}$ does not appear in $S$, which is a contraction. So $C$ must be uncountable.

0과 1사이의 실수의 개수를 구하여라

1. We can represent a real number between 0 and 1 using a binary system.
   $r_1 = 0.d_{11}d_{12}d_{13}... $
   $r_2 = 0.d_{21}d_{22}d_{23}... $
   $r_3 = 0.d_{31}d_{32}d_{33}... $
   where $d_{ij} \in \left \{0, 1 \right \}$.
2. To fully distinguish a real number $r_i$, we need $ℵ_0$ bits where $ℵ_0$ is the number of all integers.
3. Consequently, $c = 2^{ℵ_0}$ (uncountable).

Set 용어(2)

• function or mapping (함수) $f : U → V$
• domain (정의역) $U$, codomain (공역) $V$
• image (상) $f (A) = {f (x) ∈ V : x ∈ A}, A ⊆ U$
• range  (치역) $f (U)$
• inverse image or preimage (역상) $f ^{−1} (B) = {x ∈ U : f (x) ∈ B}, B ⊆ V$ (우리가 AI를 통해 구하고자 하는 것은 대부분 이것)

*정의역의 상을 치역이라고 한다. 반대로, 공역의 원상은 항상 정의역이다.

• one-to-one or injective (일대일 함수): $f (a) = f (b) ⇒ a = b$
• onto or surjective: $f (U) = V$
• invertible (일대일 대응,  전단사 함수(bijection, bijective function)): one-to-one and onto

bijection일 경우, x와 y의 cardinality가 같다.

Measure theory

학습목표

수학자들이 세상을 만들어가는 과정을 생각해보면, 
먼저 Set을 정의하고 여기서 더 나아가 각각의  Set에 대한 Measure를 정의합니다.
지난 시간에 Set theory를 공부하면서 Set에 대해서 알아보았으니
이번 시간에는 Set에 대한 Measure를 정의해보면서 확률에 대해서 이해하기 위해 한걸음 다가가봅시다.

 

핵심 키워드

• 측도론(Measure theory)
• 측도(Measure)
• Set function
• Sigma field
• Measurable space

Given a universal set U, a measure assigns a nonnegative real number to each subset of U

(사람들의 집합이 있다면 몸무게를 measure 해보고 싶은 것)

• set function: a function assigning a number of a set (example: cardinality, length, area, [즉, set에 대해 숫자를 매기는 것]).
• $\sigma$-field ${\mathcal {B}}$: a collection of subsets of U such that (axioms) (대표적으로 power set이 있다)
  1. $\varnothing \in {\mathcal {B}}$ (empty set is included.)
  2. $B \in \mathcal{B} \Rightarrow B^c \in \mathcal{B}$ (closed under set complement.) (100명 중 2명에 대해 몸무게를 잴 수 있으면, 나머지 98명에 대해서도 잴 수 있어야한다)
  3. $B_i \in \mathcal{B} \Rightarrow \cup ^\infty_{i=1} B_i \in \mathcal{B}$ (closed under countable union.) (2명을 합친 몸무게를 잴 수 있어야한다)
  
  • properties of $\sigma$-field ${\mathcal {B}}$
    1. $U \in \mathcal{B}$ (entire set is included.) (위의 1,2 번 특성을 합치면 성립한다, empty set의 complement set)
    2. $B_i \in \mathcal{B} \Rightarrow \cap ^\infty_{i=1} B_i \in \mathcal{B}$(closed under countable intersection)
    3. $2^U$ is a $\sigma$-field. (power set)
    4. $\mathcal{B}$ is either finite or uncountable, never denumerable. (set이 $ℵ_0$개면 $\sigma$-field는 $2^{ℵ_0}$ 이기 때문에 uncountable 즉, denumerable하지 않다)
    5. $\mathcal{B}$ and $\mathcal{C}$ are $\sigma$-fields $\Rightarrow \mathcal{B} \cap \mathcal{C}$ is a $\sigma$-field but $\mathcal{B} \cup \mathcal{C}$ is not.
    • $\mathcal{B} =\left\{ \varnothing , \left\{ a \right\}, \left\{ b,c \right\}, \left\{ a,b,c \right\}\right\}$
    • $\mathcal{C} =\left\{ \varnothing , \left\{ a,b \right\}, \left\{ c \right\}, \left\{ a,b,c \right\}\right\}$
    • $\mathcal {B} \cap \mathcal{C} =\left\{ \varnothing ,  \left\{ a,b,c \right\}\right\}$ (this is a $\sigma$-field)
    • $\mathcal{B} \cup \mathcal{C} =\left \{ \varnothing , \left\{ a \right\}, \left\{ c \right\}, \left\{ a,b \right\}, \left\{ b,c \right\}, \left\{ a,b,c \right\}\right\}$
      (this is not a $\sigma$-field as $\left\{ a,c \right\} = \left\{ a\right\} \cap \left\{ c\right\}$ is not included.)

$\sigma (\mathcal {C})$ is called the $\sigma$-field generated by $\mathcal{C}$. ($\mathcal{C}$로부터 생성한 $\sigma$-field)

A $\sigma$-field is designed to define a measure.
($\sigma$-field는 measure를 하기 위해 정의되며 Kolmogorov가 주장한 것은 $\sigma$-field에서 measure가 probability measure가 된다.)
If the element is not inside a $\sigma$-field, it cannot be measured.
(결과적으로 $\sigma$-field 안에 없다면 값이 0이 아니라 measure될 수가 없다)

• A set $U$ and a $\sigma$-field of subsets of $U$ form a measurable space $(U, \mathcal{B})$. (set과 $\sigma$-field로 measurable하게 만들면 그것이 measurable space이다) 
• A measure $\mu$ defined on a measurable space $(U, \mathcal{B})$ is a set function
  $\mu : \mathcal{B} \rightarrow [0,\infty]$ such that (measure는 0이상이다)
  1. $\mu(\varnothing) = 0$
  2. For disjoint $B_i$ and $B_j \Rightarrow \mu (\cup^\infty_{i=1}B_i)=\sum^\infty_{i=1}\mu(B_i)$ (countable additivity) (각각의 measure를 재서 더한 값 = 합쳐서 measure한 값)
• Probability is a measure such that $\mu(U)=1$ i.e., normalized measure. (전체가 1이되는 normalized measure가 확률이다)
• A measurable space $(U, \mathcal{B})$ and a measure $\mu$ defined on it together
  form a measure space $(U, \mathcal{B}, \mu)$. (set이 있고 $\mu$로 정의되는 subset들의 집합 $\sigma$-field가 있고 양수인 숫자를 부여할 수 있는 measure가 있고 그 값이 위의 두 조건을 만족하면 measure space가 된다)