지난 강의에 이어
○NLP에서의 재귀(recurrent) 모델
2016년을 전후로, NLP의 사실상의 전략은 다음과 같다.

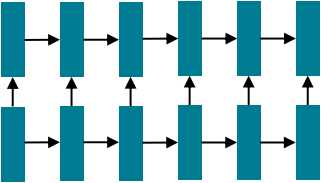
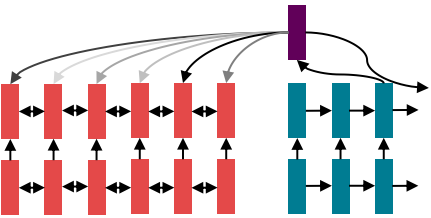
이번 시간에는 색다른 것을 배운다기보다 모델에서 최적의 building blocks가 뭔지 찾아볼 것이다.

○ RNNs의 문제: 선형 상호작용 거리 (Linear interaction distance)
RNNs은 "왼쪽에서 오른쪽으로" 전개되며 이는 선형 인접성을 인코딩한다

그러나 문제는 RNNs이 거리가 떨어진 단어간 상호작용하려면 O(시퀀스 길이) step이 필요하다

먼 거리 의존성은 기울기 소실 문제 때문에 제대로 학습하기 어렵다. 단어의 선형 순서는 우리가 집어넣은 것으로 우리는 문장을 생각할 때 순서대로 보지 않는다.

○ RNNs의 문제: 병렬화의 부재
앞 혹은 뒤로의 흐름은 O(시퀀스 길이) 비병렬 연산을 수행해야 한다.
GPU는 한 번에 많은 독립적인 계산을 수행할 수 있으나 과거의 RNN hidden states가 계산되기 전에는 미래의 RNN hidden states를 계산할 수 없다.
이 때문에 매우 큰 데이터 세트에 적용할 수 없다.

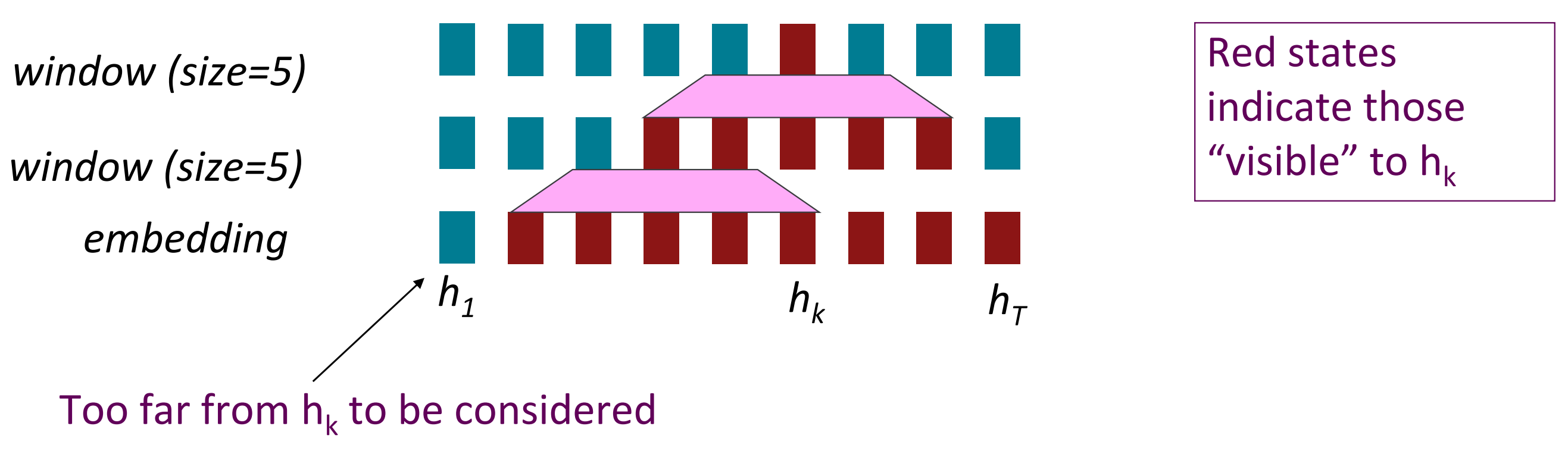
○ 재귀가 아니라면 word window는?
word window를 사용 시 시퀀스의 길이에 비례해서 비병렬 연산을 수행하지 않아도 된다.

word window는 주변 문맥을 모아서 볼 수 있기 때문에 층을 더 많이 쌓을 수록 이론상 더 많은 단어간 상호작용을 고려할 수 있다.
Maximum interactioin distance = sequence length / window size
이론상 멀리까지 볼 수는 있지만 여전히 거리에 의한 제한이 존재하는 것은 사실이다.
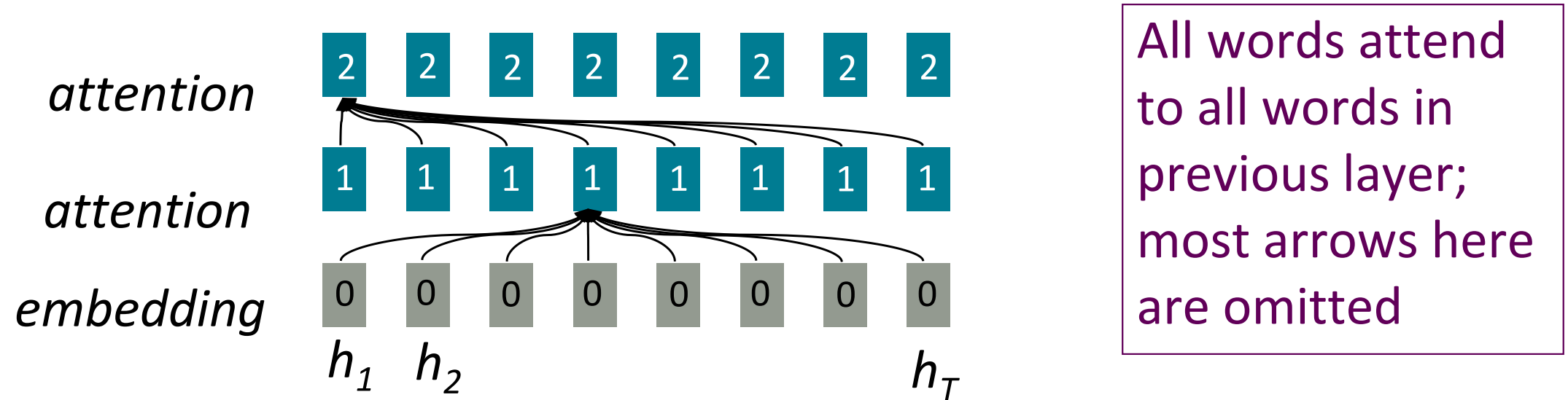
○ 재귀가 아니라면 어텐션은?
어텐션의 경우 각 단어의 representation에 query로 접근하여 values의 집합에서 정보를 얻는가져온다. 이전에 우리는 decoder에서 encoder로 어텐션했지만 이번에는 단일 문장에 대해 생각해보자. 어텐션을 사용하면 문장 길이에 따른 비병렬화 문제는 해결된다. Maximum interaction distance= O(1) 모든 단어가 모든 층에서 서로 상호작용한다.
○ 셀프 어텐션(Self-Attention)
어텐션 연산을 위해서는 queries, keys, values가 필요하다.
- queries $q_{1}, q_{2},...,q_{T}$. 각 query는 $q_{i} \in \mathbb{R}^{d}$
- keys $k_{1}, k_{2},...,k_{T}$. 각 key는 $k_{i} \in \mathbb{R}^{d}$
- values $v_{1}, v_{2},...,v_{T}$. 각 value는 $v_{i} \in \mathbb{R}^{d}$
- self-attention에서 queries, keys, values는 같은 source에서 생성된다.
만약 이전 층의 출력이 $x_{1}, x_{2},...,x_{T}$ (단어 당 벡터 하나) 라면, $v_{i}=k_{i}=q_{i}=x_{i}$로 모두 같은 벡터이다.

Q) Fully connected layer와의 차이점은?
Fully connected layer에서는 임의의 가중치를 설정해서 모델이 스스로 어떤 단어들 간의 상관성을 학습해야하므로 학습이 느리다. 그러나 self-attention의 경우 모든 매개변수가 입력과 관계되어 있으며, 내적으로 연산을 수행하므로 층간에 모두 연결되지 않고 중요한 정보에 집중해서 층이 연결된다.
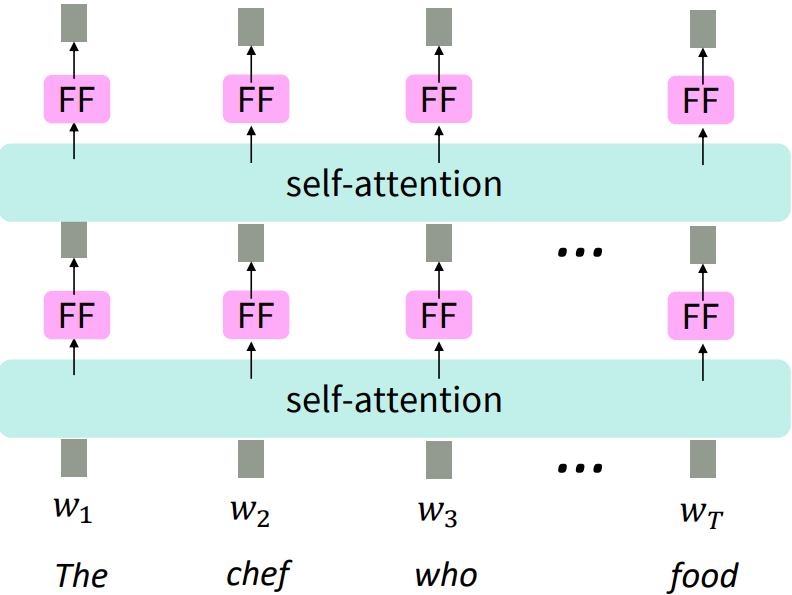
○ NLP building block으로의 셀프 어텐션(Self-Attention)

LSTM을 쌓았던 것과 같이 그림에서 self-attention block을 쌓았다. self-attention은 집합으로서 연산되기 때문에 순서에 대한 정보가 누락되어 있다. 다시말하면 단어간 배열을 바꾸어도 똑같은 결과를 준다.
만약 sequence index를 벡터로 표현한다면, 위치 벡터(position vector) $p$는 다음과 같다
$$p_{i}\in \mathbb{R}^{d}, i \in \{1,2,...,T\}$$
이를 keys, queries, values에 반영하기위해 간단하게 더해보자
$$k_{i}=\tilde{k_{i}}+p_{i}$$
$$q_{i}=\tilde{q_{i}}+p_{i}$$
$$v_{i}=\tilde{v_{i}}+p_{i}$$
깊은 self-attention 에서 우리는 첫 층에 위의 연산을 수행하며 단순히 concatenate 해줄수도 있지만, 일반적으로 그냥 더한다.
위치벡터는 어떻게 생성하면 좋을까?
Sinusoidal position representations: 변화하는 주기에 따른 삼각함수를 연결해준다.

장점)
주기를 가진다는 뜻은 "절대 위치"는 중요하지 않다는 것을 뜻한다.
주기의 재시작을 이용하기 떄문에 더 긴 시퀀스에도 적용가능하다.
단점)
학습이 불가능하며 실제로 긴 시퀀스에 적용이 잘 안된다.
*실제로 슬라이딩한 문장을 넣으면 생각보다 위치에 대한 의미 반영이 잘 안된다.
Learned absolute position representation: 모든 $p_{i}$를 학습가능한 매개변수로 놓자. 행렬 $p \in \mathbb{R}^{d\times T}$ 를 학습하고 각 $p_{i}$가 해당 행렬의 열이 되도록한다.
장점)
유연성: 각 위치는 데이터로 부터 학습된다
단점)
길이에 대한 확장이 불가능하다
*학습한 문장보다 더 긴 문장을 넣을 수 없다.
대부분 시스템은 이 방식을 사용한다.
그 외에 사람들은 더 유연한 position representation을 사용하려고 시도했다.
- Relative linear position attention [Shaw et al., 2018]
- Dependency syntax-based position [Wang et al., 2019]
self-attention 에서의 비선형
단순하게 feed-forward network를 각각의 output vector에 더해주면 된다
$$m_{i}=MLP(output_{i})=W_{2}\times ReLU(W_{1}\times output_{i} + b_{1}) +b_{2}$$
결과적으로 어텐션의 결과를 feed-forward network의 입력으로 받는다.
시퀀스(문장)를 예측할 떄 미래를 보지 않는다는 보장이 필요하다.
미래를 예측하는 기계번역이나 언어모델에서 미래를 보면 안된다.
따라서 미래를 Masking 한다.
기계 번역의 경우 encoder를 self-attention으로 설정하고 bi-directional LSTM을 decoder로 사용한 이유는 모델이 실제 예측 단계에서 미래를 보지 않기 때문이다. 따라서 decoder로 self-attention을 사용하기 위해서는
1. 매 timestep마다 과거의 정보만 가지도록 keys와 values를 변화시킨다. (비효율적)
2. 병렬화를 위해서 미래 단어의 attention score를 -∞로 mask out 해준다.

결론
- Self-attention
- Position representations
- Self-attention은 unordered function이므로 시퀀스 순서를 구체화하여 입력한다
- Nonlinearities
- Self-attention의 출력 부분에 단순한 feed-forward network를 추가한다
- Masking
- 미래를 보지 않는 병렬 연산을 수행하기 위해서 수행. 미래의 정보가 과거로 세지 않도록 한다.
○ The Transformer Encoder-Decoder [Vaswani et al., 2017]

Transformer Encoder Block에서 다루지 않는 내용
- key-query-value attention: 어떻게 한 단어에서 k, q, v 단어 임베딩을 수행하는가?
- Multi-headed attention: 하나의 층에서 여러 곳으로 입력
- 훈련에 도움되는 trick: 해당 trick들은 모델이 하는 일을 향상시키지는 않지만 훈련 과정을 향상시킨다.
- Residual connections
- Layer normalization
- Scaling the dot product
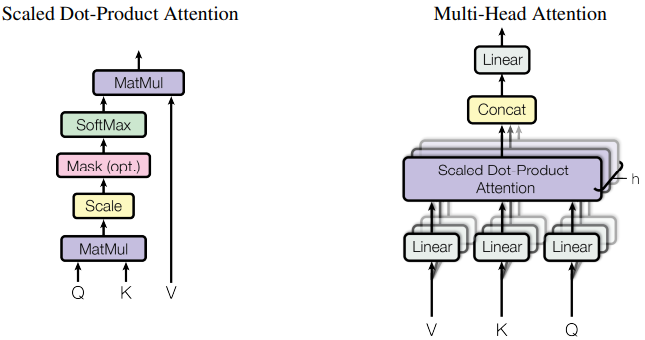
○ The Transformer Encoder: Key-Query-Value Attention 연산
$x_{1},...,x_{T}$ 를 Transformer encoder의 입력 벡터라고 하자, ($x_{i}\in\mathbb{R}^{d}$)
- $K\in\mathbb{R}^{d\times d}$, 일 때 $k_{i}=Kx_{i}$ 이고 key 행렬이다.
- $Q\in\mathbb{R}^{d\times d}$, 일 때 $q_{i}=Qx_{i}$ 이고 query 행렬이다.
- $V\in\mathbb{R}^{d\times d}$, 일 때 $v_{i}=Vx_{i}$ 이고 value 행렬이다.
이 때 연산이 어떻게 되는지 학인해보자
$X=[x_{1},...,x_{T}]\in \mathbb{R}^{T\times d}$라고 연결된 입력 벡터라고 하자,
먼저 $XK\in\mathbb{R}^{T\times d}, XQ\in\mathbb{R}^{T\times d}, XV\in\mathbb{R}^{T\times d}$이며,
출력 = $\texttt{softmax}(XQ(XK)^{T})\times XV$

○ The Transformer Encoder: Multi-headed attention
만약 문장 안에서 여러 곳을 한번에 집중하고 싶다면?
단어 i에 대해, self-attention은 $X_{i}^{T}Q^{T}Kx_{j}$이 큰 곳을 집중하지만 만약 다른 이유로 다른 j에 집중하고 싶다면 어떻게 할까?
Multiple attention "heads" 를 Q,K,V 행렬에 추가한다.
$Q_{l}, K_{l}, V_{l}\in \mathbb{R}^{d\times \frac{d}{h}}$ 라 하자, h는 어텐션 heads의 숫자이고, $l$은 $1$~$h$의 범위를 가진다.
각 어텐션 head는 어텐션 연산을 각각 수행한다:
$$\texttt{output}_{l} = \texttt{softmax}(XQ_{l}K_{l}^{T}X^{T})*XV_{l}, \texttt{output}_{l}\in \mathbb{R}^{\frac{d}{h}}$$
다음 어텐션 head의 결과를 모두 합친다!
$$\texttt{output}_{l} = Y[\texttt{output}_{1},..,\texttt{output}_{h}], Y\in\mathbb{R}^{d\times d}$$
각 head는 각기 다른 것에 집중하며 벡터를 각각 다르게 생성한다.

○The Transformer Encoder: Residual connections [He et al., 2016]
Residual connections는 모델의 학습을 도와주는 trick이다.
i가 특정 층이라고 할 때 $X^{(i)} = \texttt{Layer}(X^{(i-1)})$ 를 사용하는 대신에 다음을 사용한다
$$X^{(i)} = X^{(i-1)}+\texttt{Layer}(X^{(i-1)})$$
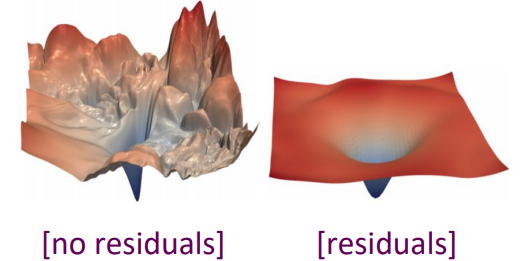
이 기법을 이용하면 신경망이 깊어질 때 발생하는 기울기 소실 문제를 완화할 수 있다. Loss landscape 그림을 보면 residual connection을 적용하면 훨씬 표면이 부드러워지는 것을 확인할 수 있다. 따라서 학습에서 모델이 global minimum을 찾아가는 것이 훨씬 용이하다.
○The Transformer Encoder: Layer normalization [Ba et al., 2016]
Layer normalization 은 학습을 빠르게 해주는 trick이다.
Idea: 은닉 벡터의 불필요한 정보 변동을 표준화를 통해 제거해준다.
(LayerNorm 이 효과적인 이유는 기울기 표준화 때문이다. [Xu et al., 2019])
모델의 개별 단어 벡터를 $x\in \mathbb{R}^{d}$, 가중치를 $\gamma \in \mathbb{R}^{d}$, 편차를 $\beta \in \mathbb{R}^{d}$ 라 하자,
평균을 $\mu$ 표준편차를 $\sigma$라고 할 때,
$$ \texttt{output} = \frac{x-\mu}{\sigma+\epsilon}*\gamma + \beta $$
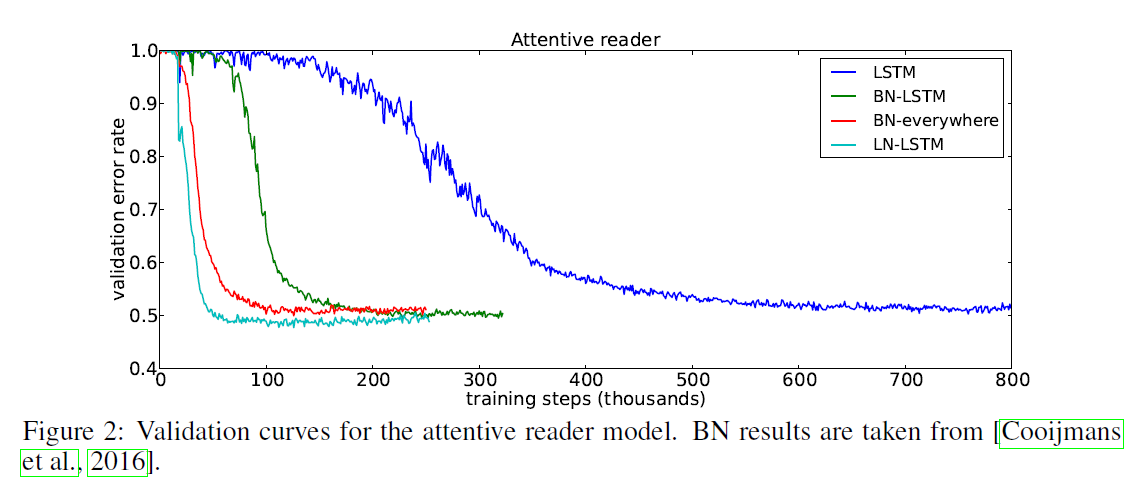
Batch normalization과의 차이점)
Batch normalization의 경우 batch 크기에 의존하며, recurrent 기반 모델에 적용이 어렵다. 기본적으로 입력이 sequence이기 떄문에 batch normalization을 위해서는 매 timestep마다의 평균과 분산을 저장하여 적용해야하기 때문에 구현에 어려움이 존재한다.
따라서 batch 크기에 의존하지 않으며 sequence 길이에도 영향을 받지 않는 방법이 layer normalization이다.
○The Transformer Encoder: Scaled Dot Product [Vaswani et al., 2017]
어텐션 score를 계산할 때 dot product 연산에서 차원 $d$가 증가함에 따라 그 값은 점점 커진다. score 값이 커지면 softmax 값의 일부 값이 굉장히 커지게 되고 낮은 확률을 지니고 있던 값들도 그 값이 너무 작아져 기울기 값이 0으로 수렴하게된다.
$$\texttt{output}_{l} = \texttt{softmax}(XQ_{l}K_{l}^{T}X^{T})*XV_{l}), \texttt{output}_{l}\in \mathbb{R}^{\frac{d}{h}}$$
따라서 위의 self-attention 함수에서 attention score를 $\sqrt{d/h}$ 해주어 차원 의존도를 없애준다.
$$\texttt{output}_{l} = \texttt{softmax}(\frac{XQ_{l}K_{l}^{T}X^{T}}{\sqrt{d/h}})*XV_{l}, \texttt{output}_{l}\in \mathbb{R}^{\frac{d}{h}}$$
*q와 k는 평균이 0 분산이 1이므로, $q\cdot k = \sum^{d_{k}}_{i=1}q_{i}k_{i}$의 평균은 0 그리고 분산은 $d_{k}$가 된다.
○ The Transformer Encoder-Decoder [Vaswani et al., 2017]
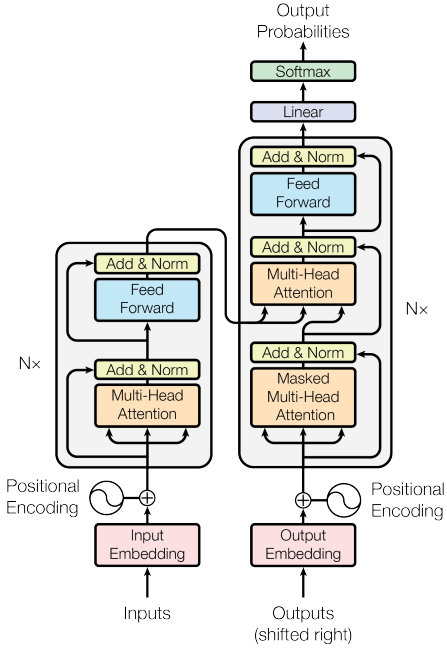
다시 모델 구조로 오면 매 층마다 residual과 layer normalization을 수행하며 feed forward는 attention 연산이 완료된 후에 적용한다. 이 때 encoder의 경우 단순 multi-head attion을 적용하고 decoder의 경우 미래를 추론하는 작업이기 때문에 미래에 대해서는 masking 된 attention을 적용한다. 이후 출력값을 encoder의 출력값과 합쳐서 attention 연산을 수행하는데 소위 cross-attention이라 하는 이 부분을 다뤄보도록하자.
*위의 그림에서 Nx로 되어 있는 부분을 통해 알 수 있듯이 해당 block을 여러번 쌓을 수 있다. 이 때 encoder의 경우 최종 출력값을 이용해 cross-attention에 넣어주는데 그 이유는 각각 attention 출력을 decoder에 넣어주려면 우선 숫자가 같아야 구현이 용이하기 때문이다.
○The Transformer Decoder: Cross-attention (details)
지금까지 우리는 self-attention에서 keys, querys, values를 같은 모두 소스로부터 가져오는 것을 보았다. Decoder에서는 지난주 RNN어텐션에서와 유사한 작업을 수행한다.
- Transformer encoder의 출력 벡터를 $h_{1},...,h_{T}$ 라고 놓자. 이 때 $h_{i}\in \mathbb{R}^{d}$
- Transformer decoder의 입력 벡터를 $z_{1},...,z_{T}$ 라고 놓자. 이 때 $z_{i}\in \mathbb{R}^{d}$
(* 입력 벡터: decoder의 입력층에 가까운 multi-head attention의 출력값) - Keys와 values는 (메모리와 같이) encoder로부터 가져온다
: $k_{i}=Kh_{i}, v_{i}=Vh_{i}$ - Quries는 decoder로부터 가져온다.
: $q_{i}=Qz_{i}$ - Keys, queries, values가 정의되었으므로 cross-attention 연산을 수행해보자
- Encoder 벡터를 연결하여 $H=[h_{i},...,h_{T}]\in \mathbb{R}^{T\times d}$라 하자.
- Decoder 벡터를 연결하여 $Z=[z_{i},...,z_{T}]\in \mathbb{R}^{T\times d}$라 하자.
*연산의 편의성을 위해 같은 H와 Z를 같은 T차원으로 정의 - Cross-attention 출력: $\texttt{output}=\texttt{softmax}(ZQ(HK)^{T})\times HV$
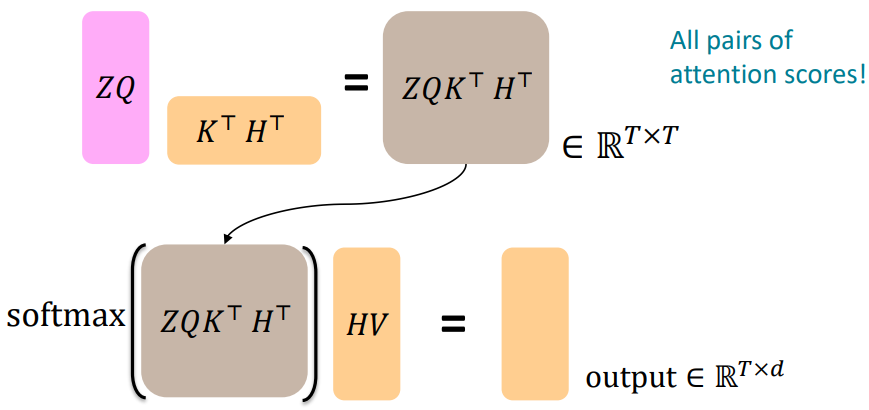
○Great Results with Transformers
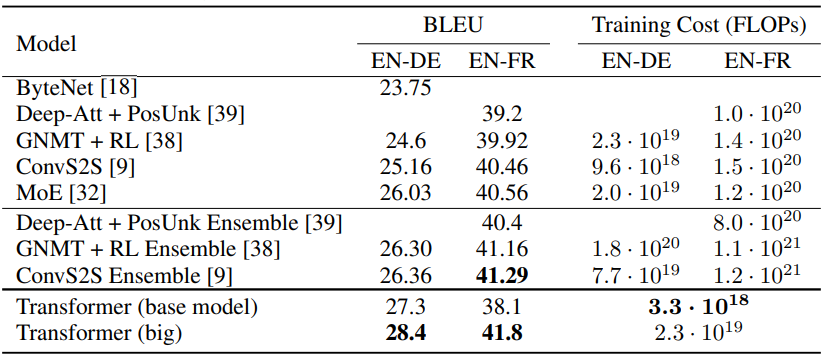
Transformer는 기계번역에서 높은 성능 뿐만아니라 훨씬 효율적인 훈련이 가능하다.

문서 생성에서도 기존의 RNN 계열의 seq2seq-attention보다 훨씬 상회하는 성능을 보여주었다.
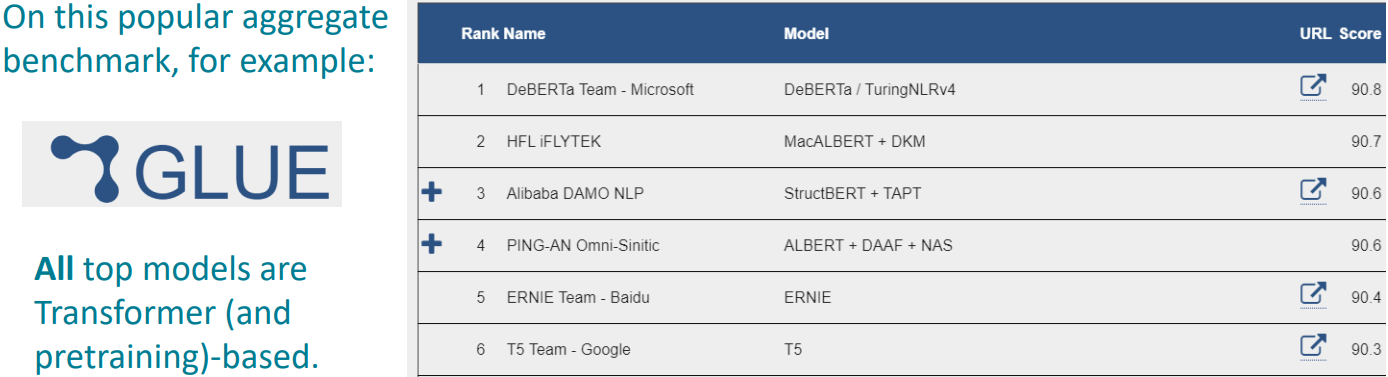
GLUE 순위표도 얼마 지나지 않아 모두 transformer 기반의 모델들이 상위권을 차지하였다.
○Transformer에서 개선할 점
- Self-attention에서의 이차함수적 연산량
- 모든 짝의 상호작용을 연산한다는 것은 문장의 길이에 이차함수적으로 연산량이 증가한다는 것을 의미한다
- 재귀 모델에서는 선형적으로 증가
- Position representations
- 간단하게 절대적인 색인을 사용하는 것이 최선의 방법인가?
- Relative linear position attention [Shaw et al., 2018]
- Dependency syntax-based position [Wang et al., 2019]
○시퀀스 길이의 대한 이차함수
Transformer의 총 연산량은 $O(T^{2}d)$로 증가한다. 이 때 T는 시퀀스 길기, d는 차원이다.
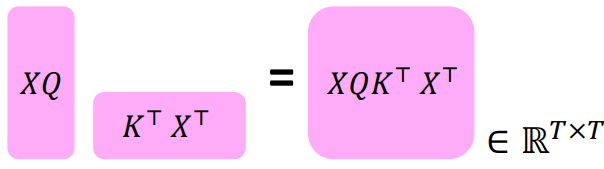
d가 1000이라고 할 때,
짧은 문장인 $T<30; T^{2}<900$
실제로는 $T=512$로 많이들 제한하곤 한다.
만약 $T>10000$ 을 연산하고 싶다면 어떻게 할까? 예를 들어 긴 문서의 경우
Linformer [Wang et al., 2020]
Keys, Values에 대한 시퀀스 길이 차원(T)를 더 작은 차원으로 사영시킨다. 오른쪽 그래프에서 확인할 수 있듯이 문서의 길이가 길어져도 연산량이 선형으로 증가한다.
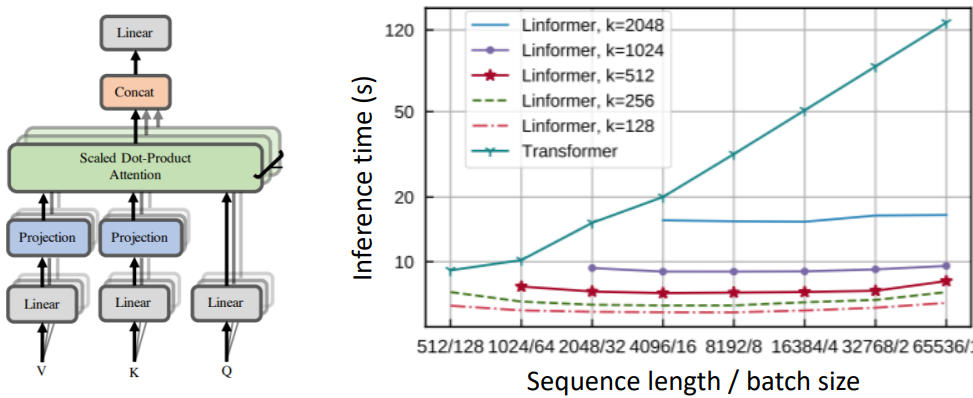
BigBird [Zaheer et al., 2021]
모든 쌍의 상호작용을 다양한 방식으로 간략화한다. (Random attention, Local window, looking at everything)
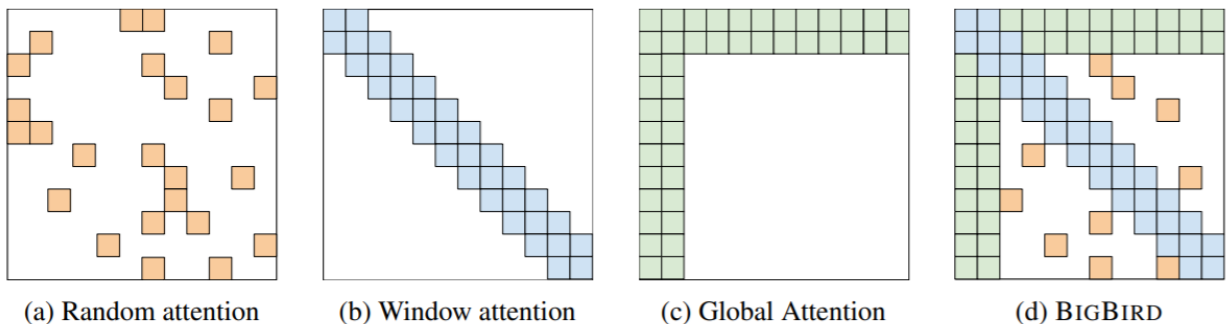
Q) RNN이 transformer보다 좋을 때는?
강의 A) 일부 강화학습이나 transformer는 많은 데이터를 필요로하므로 데이터 량이 적을 때 유용할 수 있다.
추가 A) 요즘엔 transformer 위에 RNN-CRF를 올려서 좋은 성능을 뽑은 모델이 많으며, 용도에 따라 적절하게 사용할 수 있다.
Reference)
Slide: PowerPoint Presentation (stanford.edu)
Video: Stanford CS224N NLP with Deep Learning | Winter 2021 | Lecture 9 - Self- Attention and Transformers - YouTube
'교육 > CS224N winter 2021' 카테고리의 다른 글
| Clean your desk! Transformers for unsupervised clustering of document images (0) | 2023.09.25 |
|---|---|
| Lec10) Transformers and Pretraining (0) | 2022.07.05 |
| Lec 8) Attention (0) | 2022.06.16 |
| Lec 7) Translation, Seq2Seq (0) | 2022.06.14 |
| Lec 6) Simple and LSTM RNNs (0) | 2022.05.18 |



