Lec2) Neural Classifiers

 

이전 강의: https://enjoythehobby.tistory.com/entry/Lec1-Word-Vectors

Lec1) Word Vectors

○ Word2vec 복습

• 임의의 단어 벡터로 시작
• 주어진 중심단어에 대한 주변 단어 확률($P(o|c)$) 예측을 수행
• 전체 말뭉치(corpus)의 각 단어에 대해 반복수행

$P(o|c)=\frac{\texttt{exp}(u_{o}^{T}v_{c})}{\sum_{w\in V} \texttt{exp}(u_{w}^{T}v_{c})}$

 

중심 단어 'into'에서 window 크기 2의 주변 단어 발생 확률

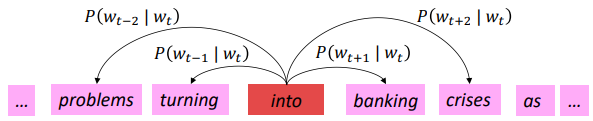
• 학습(Learning) : 예측이 좋아지는 방향으로 단어 벡터를 update
• 이것만으로 단어공간(wordspace)에서 단어 간 유사도와 의미의 방향을 잘 정의한다

○ Word2vec 매개변수 와 계산

word2vec의 단어 벡터와 4번째 중심 단어에 대한 확률 계산

word2vec의 경우 문장에서의 단어 순서에 상관없이 항상 같은 확률을 예측한다. ▶ "Bag of words" 모델

문맥에서 중심 단어에 대한 주변 단어 발생 확률에 대해 높은 확률을 부여하고자 한다. (적게 발생하는 빈도에 대해서도)

▶ 이를 위해서는 고차원 단어공간에서 서로 가깝게 배치해야 한다. (내적 값이 커야하므로 당연하다)

2차원으로 투영한 단어 벡터의 분포 유사한 단어끼리 인접한 것을 확인할 수 있다. (빨간원)

---

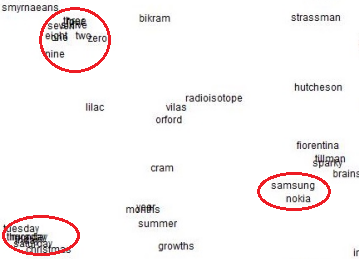
최적화(Optimization): 경사하강법(Gradient Descent)

○ 좋은 단어 벡터는 어떻게 학습하는가?

지난 시간에 손실 함수 $J(\theta)$의 값을 최소화하기 위해 미분하는 것을 살펴봤습니다. 여기서는 미분 이후의 작업에대해 기술합니다.

경사하강법(Gradient Descent): 0에 가까운 임의의 벡터로 시작(Initialize)하여 $J(\theta)$에서 $\theta$를 반복적(Iterative)으로 변화를 주어 최솟값에 근접하게 합니다.

이 때 현재 $J(\theta)$의 미분값이 0에 가까워지는 방향으로 $\theta$에 적절하게 작은 변화(step)를 줍니다.

• 변화량이 작을 경우: local minima에 수렴할 수 있으며 최적화에 시간이 오래 걸린다
• 변화량이 클 경우: 아래 그림처럼 큰 변화량에서는 최적화가 힘들고 값이 발산(Diverge)할 수 있다.

경사하강법으로 매개 변수를 변화시키는 과정, 이해를 돕기위해 2차 곡선으로 그려졌다.

미분값($\bigtriangledown_{\theta}J(\theta)$)을 반영한 매개변수 update 방법은 아래와 같다.

$\theta^{new}=\theta^{old}-\alpha\bigtriangledown_{\theta}J(\theta)$

*여기서 $\alpha$는 step size 또는 학습률(learning rate)이라고 한다.

while True:
    theta_grad = evaluate_gradient(J,corpus,theta)
    theta = theta - alpha * theta_grad

그러나 이 방식은 전체 말뭉치(corpus)에 대해 수행되므로 이는 너무 비용이 많이 들어 실제 사용되지 않는다.

 

확률적 경사하강법(Stochastic Gradient Descent, SGD): 일부 window에 대해 한개 혹은 작은 배치(batch)에 대해 매개변수를 update한다.

while True:
    window = sample_window(corpus)
    theta_grad = evaluate_gradient(J,window,theta)
    theta = theta - alpha * theta_grad

이 방식을 통해 적은 연산량으로 빠르게 손실 함수를 최적화 시킬 수 있으며, 학습 과정이 진폭이 크고 불안정해 보이지만 global minima를 찾는 성능면에서는 더 우수할 수 있다.

특정 window에 대해 SGD를 수행할 경우 중심단어를 포함하여 $2\times \texttt{window} + 1$개의 단어에 대해서만 매개변수를 update하게며 이는 전체 말뭉치 크기에 비해 굉장히 좁은 영역입니다.

* 실제 deep learning 패키지에서 단어는 지금까지 설명과 달리 열이 아니라 행에 위치한다. 따라서 해당 단어의 행을 U와 V 행렬에대해 update해주면 된다.

---

○ Word2vec algorithm family: More details 

왜 벡터를 중심 단어와 문맥 단어 두 개 사용하는 이유: 쉬운 최적화, 마지막에 둘을 평균내어 사용

* 단어 하나 당 하나의 벡터를 사용할 수 있고 성능도 약간 좋지만 동일 단어가 중심 단어와 문맥 단어에 발생했을 때 algorithm 구현이 복잡해진다.

1. Skip-grams(SG)
   중심 단어로부터 문맥 단어를 예측 (지금까지 설명에서 예시로 사용)
2. Continuous Bag of Words(CBOW)
   문맥 단어로부터 중심단어를 예측

○ 효율적인 학습을 위해

지금까지 naive softmax(simple, expensive)를 사용하였지만 네거티브 샘플링(Negative sampling, NS)을 word2vec 저자인 Mikolov는 추천한다

naive softmax가 비효율적인 이유는 분모($\sum_{w\in V} \texttt{exp}(u_{w}^{T}v_{c})$)에서 모든 단어에 대해 내적을 해주기 때문이다. 그래서 이진 로지스틱 회귀(binary logistic regression)을 true pair(중심 단어와 window 내 문맥 단어) 대 noise pair(중심 단어와 임의의 단어)에 수행한다.

다음 목적 함수를 최대화 하는 방향으로 최적화를 진행한다.

$$J_{t}(\theta)=\texttt{log}\sigma(u^{T}_{o}v_{c})+\sum^{k}_{i=1}\mathbb{E}_{j \sim P(w)}[\texttt{log}\sigma(-u^{T}_{j}v_{c})]$$

로지스틱/시그모이드(sigmoid) 함수 : $\sigma(x)=1/(1+e^{-x})$

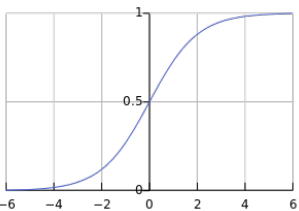
문맥 단어와 중심 단어의 확률을 최대화하기 위해 좌항은 커져야 하고, 노이즈 단어와 중심 단어의 확률을 최소화해야 한다. 여기서 우항 시그모이드 함수 안에 $-$ 를 취해주어 양항이 커지는 방향으로 함수를 조정한다.

이제 전체에 또 $-$를 취해주고 보기 쉽게 만들면 아래와 같다.

$J_{neg-sample}(u_{o},v_{c},U) = - \texttt{log} \sigma(u^{T}_{o}v_{c}) - \sum_{k\in {K \: sampled \: indices}}[\texttt{log}\sigma(-u^{T}_{k}v_{c})]$

 

상기 식에서 sampling할 때, $P(w)=U(w)^{3/4}/Z$ 수식을 이용하여 뽑는다. 여기서 $U(w)$는 unigram distribution(단어 빈도), $Z$는 단어수이다. 이를 통해 적게 등장하는 단어가 어느 정도 sampling될 수 있도록 보정할 수 있다.

---

○ Co-occurrence 갯수를 직접 센다면?

함께 나타나는 경우 word2vec과 유사하게 인접하여 등장하는 단어의 수를 세는 co-occurrence matrix $X$를 생각해 볼 수 있다. 전체 문서에 대해 수행할 수도 있고, 특정 window에 대해서 수행할 수도 있을 것이다. 문단 단위로 행렬을 생성한다면 주제에 대한 의미 분석이 가능하다.

예시) Window 기반 co-occurrence 행렬

• Window 길이 1 (5~10이 일반적)
• 좌우 대칭 (문맥 단어의 위치가 좌, 우 어디든 상관없다)
• 예시 문장
  - I like deep learning
  - I like NLP
  - I enjoy flying

위의 세 예시 문장에 대한 window 1짜리 co-occurrence 행렬

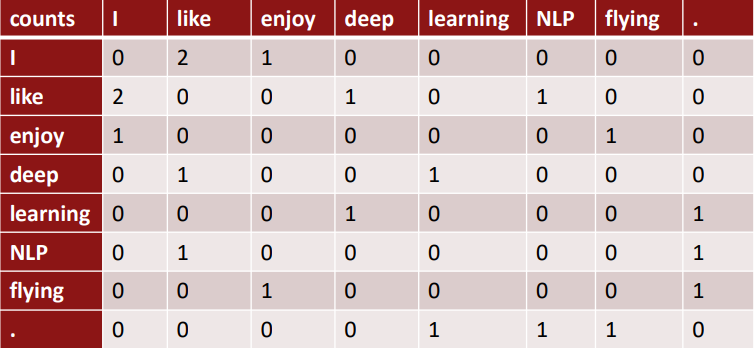
○ Co-occurrence 벡터

위 행렬로부터 co-occurrence 벡터를 생성할 수 있다. 만약 훨씬 큰 말뭉치에 대해 you가 등장한다면 I like, you like, I enjoy, you enjoy 와 같이 I와 유사한 co-occurrence 행렬값을 가질 것이며, 때문에 벡터 값도 유사하다.

 

문제점: 안의 내용은 희소한(sparse, 대부분이 0벡터) 반면에 벡터의 크기가 vocabulary에 따라 증가한다. 벡터의 희소성(sparsity)과 임의성(randomness) 때문에 모델이 노이지(noisy)하고 *강직(robust)하지 못하다.

*이상치에 영향을 덜 받는 모델을 robust하다고 한다

 

문제 해결을 위해 대부분의 중요한 정보만 남기고 저차원으로의 축소가 필요합니다.

---

○ 특이값 분해(singular value decomposition, SVD)를 통한 차원 감소

특이값 분해 관련 포스트
https://enjoythehobby.tistory.com/entry/%ED%8A%B9%EC%9D%B4%EA%B0%92%EB%B6%84%ED%95%B4Singular-Value-Decomposition-SVD

특이값분해(Singular Value Decomposition, SVD)

SVD를 통해 co-occurrence 행렬의 차원 감소를 하면 성능이 좋지 못하다. 이유는 SVD는 오차가 정규분포 한다는 가정이 들어가는데, 해당 행렬에서는 자주 등장하나 실제 의미 분석에 거의 도움을 주지 않는 'a', 'the', 'and' 와 같은불용어(stopwords) 들이 대부분이고 다른 나머지 단어들은 희박하게 등장하기 때문이다.

• 빈도에 로그(log)를 취함
• 최대값을 제한 (min(X,t), with t=100)
• 불용어를 제거

와 같은 방법을 적용한 co-occurrence 행렬에 SVD를 적용하면 모델 성능이 향상되었다.

COALS 모델 (Rohde et. al. ms., 2005), 동사에서 사람으로 의미가 유사한 벡터를 나타내는 것을 확인할 수 있다.

---

○ GloVe로 나아가기: 갯수 기반 vs. 직접 예측

갯수 기반 LSA, HAL (Lund & Burgess) COALS, Hellinger-PCA (Rohde et al, Lebret & Collobert)	신경망 기반 Skip-gram/CBOW (Mikolov et al) NNLM, HLBL, RNN (Bengio et al; Collobert & Weston; Huang et al; Mnih & Hinton)
빠른 학습 통계적으로 효율적 주로 단어를 잡는데 사용 빈출 단어에 중요도가 집중	말뭉치 크기에 비례함 통계적으로 비효율적 (중심 단어를 하나씩 확인하며 최적화) 모델의 활용도가 좋음 (다른 task에 대한 성능이 좋음) 단어 유사도 이외의 복잡한 규칙도 잡아냄

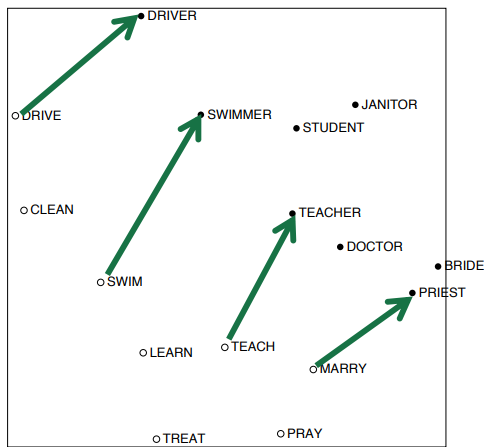
○벡터 차이에서의 의미 성분을 인코딩

주요 개념: co-occurrence 확률의 비율로 의미 성분을 인코딩

ice와 관련된 확률과 steam과 관련된 확률의 비율로 고체와 기체의 의미를 얻어낼 수 있다.

실제로 큰 말뭉치로부터 도출된 값

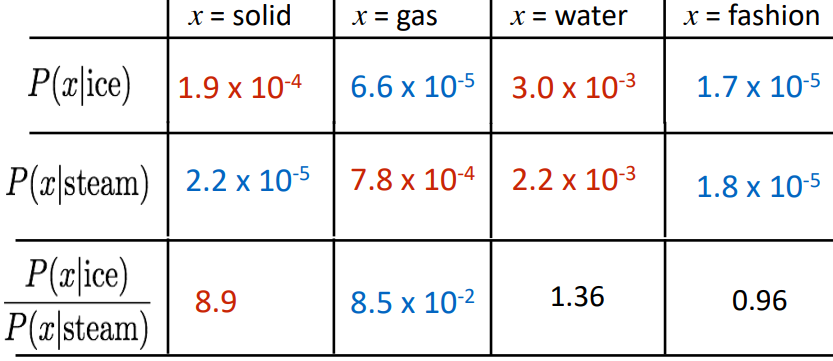
실제 위를 수식적으로 쉽게 구현하려면 확률은 Log-bilinear 모델로 구한 후 단순히 빼주면 된다.

Log-bilinear 모델: $w_{i} \cdot w_{j} = \texttt{log}P(i|j)$

벡터 차이: $w_{x} \cdot w_{a} - w_{b} = \texttt{log}\frac{P(x|a)}{P(x|b)}$

 

목적 함수 : $J = \sum_{i,j=1}^{V}f(X_{ij})(w_{i}^{T}\tilde{w_{j}}+b_{i}+\tilde{b_{j}}-\texttt{log}X_{ij})^{2}$

*연산량을 줄이고자 softmax, cross-entropy 기반에서 단어 벡터와 실제 확률의 최소제곱에 $X$를 곱해주어 의미적으로 기대값이 최소가 되도록한다는 의미가 된다

위에서 사용된 f함수, $(x/x_{max})^{\alpha}$ if $x<x_{max}$ 이외는 1

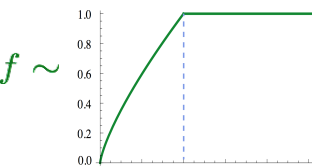
여기서 $X$는 단어-단어 co-occurrence 수이며, $P(i|j) = Xij/Xj$는 단어 $j$가 문맥 단어 $i$와 함께 등장할 확률이다.

$w$는 $d$차원의 단어 벡터이고 $\tilde{w}$는 $d$차원의 문맥 단어 벡터이다.

즉, 단어 벡터의 내적(유사도)이 co-occurrence 수의 로그값과 같아지기를 원하는 것이다.

• 빠른 학습
• 큰 말뭉치에 적용가능
• 적은 말뭉치와 작은 벡터에도 좋은 성능

GloVe로 확인한 frog 유사어

---

○어떻게 단어 벡터를 평가하는가?

내재적(Intrinsic)

• 중간/세부 하부작업(subtask)에 대해 평가
• 연산속도가 빠르다
• 시스템을 이해하는데 도움
• 실제 작업(전체 task)에 도움이 되는지는 불명확

내재적 평가 예시) 단어 벡터 유사도 

$$a:b::c:? \rightarrow d= arg\underset{i}{max} \frac{(x_{b}-x_{a}+x_{c})^{T}x_{i}}{||x_{b}-x_{a}+x_{c}||}$$

단어 벡터 간 코사인 거리가 내재하는 의미(semantic)를 잘 포착하고 구문(syntactic) 유사도 분석을 잘 수행하는지 파악한다

GloVe 내 남성, 여성 관련 단어 도시, 기울어진 정도에서 차이가 있지만 대체적으로 유사한 벡터의 차이를 보여준다.

단어 벡터 모델 유사도(Analogy) 평가 결과. 단순 SVD 성능은 굉장히 떨어지는 것이 확인 가능하다. SVD-L은 COALS와 유사한 모델이다.

다만, 모델이 성능 향상은 단순이 모델 아키텍쳐가 우수해서가 아니라 양질의 데이터가 많아진 것도 한 몫을 한다

데이터 양이 많을수록, 뉴스보단 위키피디아 데이터가 모델 성능 향상에 도움을 주었다(왼쪽). 단어 벡터의 차원이 300차원일 때부터 성능이 포화되는 것이 확인 가능하다(오른쪽).

내재적 평가 예시) 단어 벡터 거리와 사람 평가의 상관관계

WordSim353: http://www.cs.technion.ac.il/~gabr/resources/data/wordsim353/

0~10로 사람이 평가한 단어 간 유사도. 높을수록 유사하다.

데이터 셋 별 모델 평가 결과

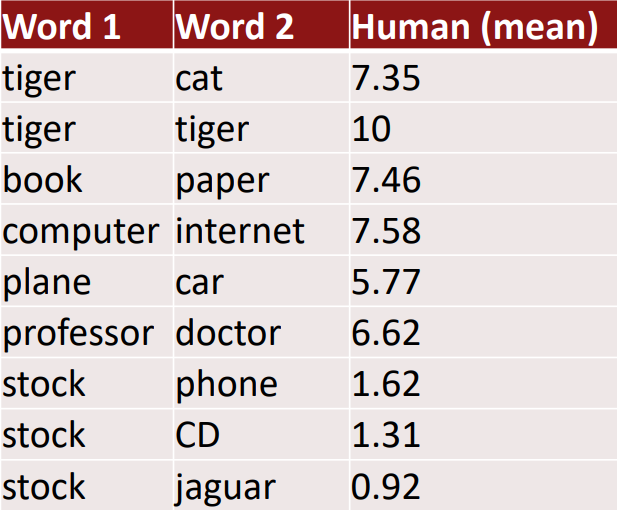
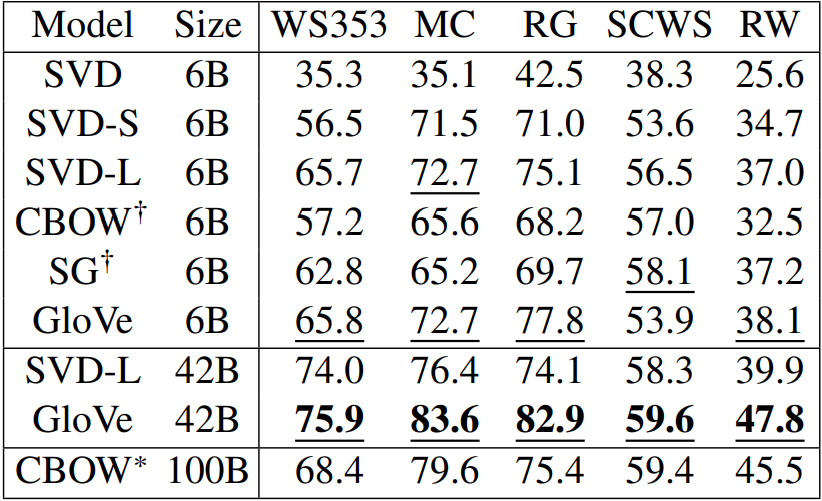
외재적(Extrinsic)

• 실제 작업에 대해 평가
• 정확한 계산에 오랜 시간이 소요
• 실제 작업 결과에 미치는 하부작업에 영향도가 불명확

외재적 평가 예시) Named entity recognition(NER): 단어를 사람, 기관, 장소 등과 같이 카테고리로 분류하여 인식

좋은 단어 벡터를 이용하면 좋은 NER 성능이 나오는가? 정답은 맞다. 좋은 단어 벡터는 단어의 뜻을 잘 표현하기 때문

모델별 NER 성능

---

○단어 의미 중의성

하나의 단어 벡터로 여러 가지 단어의 의미를 표현하는 것이 가능한가?

개념: 단어 window 별로 단어마다 클러스터링을 수행

클러스터링 결과, Improving Word Representations Via Global Context And Multiple Word Prototypes (Huang et al. 2012)

 

그러나 실용적이지 못한 방법이다. 우선 클러스터링과 단어 벡터 학습 두 단계로 작업이 진행되어야 한다는 것과 단어의 여러 의미들을 명확하게 나누기 애매하기 때문이다.

 

여러 의미 단어를 하나의 단어 벡터로 표현할 수 있을까?

개념: 다양한 의미의 단어를 선형으로 중첩시킴(linear superposition, wrighted sum)

$$v_{a} = \alpha_{1}v_{a_{1}} + \alpha_{2}v_{a_{2}} + \alpha_{3}v_{a_{3}}$$

여기서, $\alpha_{1}=\frac{f_{1}}{f_{1}+f_{2}+f_{3}}$이며 f는 빈도수(frequency)이다.

굉장히 고차원에서 희소한(sparse) 벡터를 형성하면 의미 별로 벡터를 나눌수 있게된다.

tie의 의미별 유사 단어 상위 6개,&nbsp;Linear Algebraic Structure of Word Senses, with Applications to Polysemy (Arora, &hellip;, Ma, &hellip;, TACL 2018)

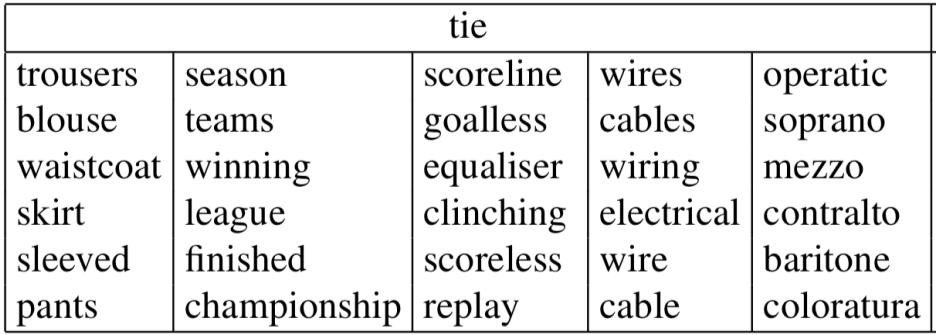
Reference)
Slide: cs224n-2021-lecture02-wordvecs2.pdf (stanford.edu)
Note: CS224n: Natural Language Processing with Deep Learning Lecture Notes: Part II Word Vectors II: GloVe, Evaluation and Training (stanford.edu)
Video: https://youtu.be/gqaHkPEZAew?list=PLoROMvodv4rOSH4v6133s9LFPRHjEmbmJ