Denotational semantics(표시적 의미론)
○ 텍스트를 분석을 위해 단어의 뜻을 어떻게 표현(represent)할 것인가?
signifier (symbol) ↔ signified (idea or thing)
표시론적 의미론에서 특정 기호(symbol)에 해당하는 개념이나 물건의 집합을 뜻(meaning)이라 할 수 있다.
위 개념을 토대로 가장 간단하게 적용한 것이 "동의어 집합(synonym set)" 과 "상위어(hypernyms)"를 이용하는 것이다. [대표 동의어사전(시소러스, thesaurus), WordNet]

○ WordNet과 같은 자원의 문제
- 늬앙스의 부재
예) "proficient"와 "good"은 동의어로 되어있지만 일부 문맥에서만 맞는말이다 - 단어의 새로운 뜻의 부재
예) wicked, badass, nifty, wizard, ninja... 등 항상 최신 상태로 단어의 뜻을 업데이트 해주는 것은 불가능 - 주관적
- 생성과 적용에 노동력이 필요
- 유사 단어를 정확하게 계산 불가 ("fantastic"과 "great"는 동의어는 아니지만 유사하다. 이를 반영할 수 있으면 deep learning에 도움이 될 것)
○ 고전적인 NLP의 문제
고전적인 NLP에서는 단어를 별개의 기호(discrete symbol)로 구분한다. 이를 지역 표상(localist representation)이라고 한다.
지역 표상의 경우 다음과 같이 원-핫 벡터(ont-hot vector)로 표현된다.
motel = [0 0 0 0 0 0 0 0 1 0 0 0]
hotel = [0 0 0 0 1 0 0 0 0 0 0 0]
그리고 해당 벡터의 차원은 단어의 수로 결정된다.
이 때 원-핫 벡터는 서로 직교(orthogonal)하기에 유사도(similarity) 비교가 불가능하다.
▶결국 유사도 비교가 가능한 벡터가 필요
Distributional semantics(분포 의미론)
○ 문맥에 따라 단어를 표현하는 방법
You shall know a word by the company it keeps, J. R. Firth 1957:11
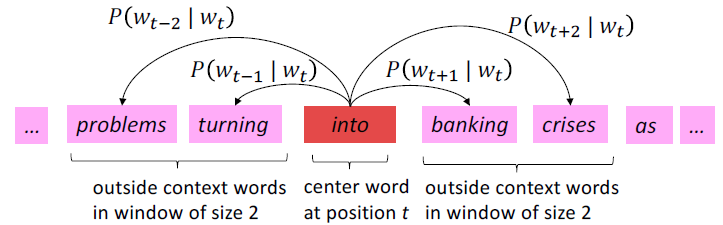
단어의 뜻은 근처에서 자주 등장하는 단어들에 의해 정해진다. 고정된 window의 주변에서 나타나는 단어들의 집합을 문맥(context)이라고 한다.
…government debt problems turning into banking crises as happened in 2009…
…saying that Europe needs unified banking regulation to replace the hodgepodge…
…India has just given its banking system a shot in the arm…
유사한 문맥에서 유사한 단어 벡터(word vector)가 보일 수 있도록 단어마다 dense 벡터로 표현되어야한다.(연속적인 실수 값을 가짐)

※Note: 분포 표현인 단어 벡터는 word embeddings 또는 word representation이라고도 불린다

○ Word2vec (Mikolov et al. 2013)
아이디어
- 큰 문서의 말뭉치 (corpus, "body"의 라틴어).
- 고정된 vocabulary에서의 모든 단어는 벡터로 표현된다.
- 문서에서의 각 위치 t를 돌아가면서 이에 해당하는 중심 단어(c, center)와 문맥 단어(o, outside)가 존재.
- 단어 벡터들 간의 유사도를 이용하여 주어진 c에 대해 o의 등장 확률을 계산한다.
- 이 확률이 최대가 되도록 단어 벡터를 최적화한다.
○ Objective(or Cost, or Loss) function
문장에서의 각 위치 $t = 1, ... , T$에서 주어진 중심 단어 $w_{j}$, 고정된 window 크기 m에서 문맥 단어의 가능도(Likelihood)는 다음과 같다
$\texttt{Likelihood}=L(\theta)= \prod_{t=1}^{T} \prod_{-m \leq j \leq m, j \neq 0}^{}P(w_{t+j}|w_{t}; \theta )$
위 수식이 최대가 되는 $\theta$(최적화 되어야하는 모든 변수)를 구해야하며 이는 편리하게 다음과 같이 변환할 수 있다.
$J(\theta)=-\frac{1}{T} \texttt{log} L(\theta)=- \frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m, j \neq 0}^{} \texttt{log}P(w_{t+j}|w_{t}; \theta )$
- $0\leq P\leq 1$이므로 log를 취해주어 계속된 소수 곱셈에 의한 underflow 방지
- $L(\theta)$가 최대가 되어야하므로 $-$를 취해주어 최소 즉 0에 가깝도록 최적화
- $T$로 나눠주어 Normalize
여기서 $P(w_{t+j}|w_{t};\theta)$를 계산하기 위해서 하기의 두 벡터를 편의 상 정의
- w가 중심 단어 일 때 벡터 $v_{w}$
- w가 문맥 단어 일 때 벡터 $u_{w}$
이 때 중심 단어 $c$에 대한 문맥 단어 $o$ $P$는 하기와 같다.
$P(o|c)=\frac{\texttt{exp}(u_{o}^{T}v_{c})}{\sum_{w\in V} \texttt{exp}(u_{w}^{T}v_{c})}$
- 내적($u_{o}^{T}v_{c}$)은 유사도를 의미하며 클수록 높은 확률을 의미한다.
- exponential은 모든 값을 양수로 변환하여 단순 크기 비교가 가능하게 해준다.
- 분모($\sum_{w\in V} \texttt{exp}(u_{w}^{T}v_{c})$)는 전체 vocabulary에 대해 normalize 해주어 확률 분포를 얻을 수 있게 해준다
이는 대표적인 softmax 함수이며, 이름의 유래는 원-핫 형태의 argmax함수를 매끄럽게 했다고 생각하면 된다. 이를 통해 미분이 용이해졌다.
○ Objective(or Cost, or Loss) function의 최솟값으로의 최적화
V만큼의 단어를 d차원의 벡터로 표현하면 단어당 $u_{w}$, $v_{w}$ 두 벡터를 가지므로 전체 $\theta$의 차원은 $\mathbb{R}^{2 d V}$가 된다. 벡터를 최적화하기 위해서는 objective function의 미분이 필요하다. 이 때 확률 $\texttt{log}P(o|c)$를 중심 단어 벡터 $v_{c}$에 대해 편미분 하면,
$\frac{\partial }{\partial v_{c}} \texttt{log} \frac{\texttt{exp}(u_{o}^{T}v_{c})}{\sum_{w\in V} \texttt{exp}(u_{w}^{T}v_{c})}$
$= \frac{\partial }{\partial v_{c}}\{\texttt{logexp}(u_{o}^{T}v_{c})- \texttt{log}\sum_{w=1}^{V}\texttt{exp}(u_{w}^{T}v_{c})\}$
좌항 $\texttt{logexp}$의 경우 사라지고 우항은 합성함수의 미분을 하면,
$= \frac{\partial }{\partial v_{c}}(u_{o}^{T}v_{c}) - \frac{\partial }{\partial v_{c}}\sum_{x=1}^{V}\texttt{exp}(u_{x}^{T}v_{c})/\sum_{w=1}^{V}\texttt{exp}(u_{w}^{T}v_{c})$
좌항은 일차함수이므로 계수인 $u_{o}$가 남고 다시 우항의 분자를 합성함수의 미분을 하면,
$= u_{o}- \sum_{x=1}^{V}\texttt{exp}(u_{x}^{T}v_{c})u_{x} /\sum_{w=1}^{V}\texttt{exp}(u_{w}^{T}v_{c})$
이 때 우항이 softmax 함수 형태로 등장하므로 $P(x|c)$ 로 표현 가능하다.
$= u_{o}- \sum_{x=1}^{V}P(x|c)u_{x}$
그러므로, 해당 수식은 관측값 $u_{o}$에서 기대값 $\sum_{x=1}^{V}P(x|c)u_{x}$를 뺀 것으로 나타난다
○ 코드 실습
Stanford 에서 제공하는 GloVe 를 gensim 패키지를 통해 word2vec 형태로 변환하여 사용해보자
word2vec 형태에서 보여지는 벡터는 일반적으로 앞서 본 중심 벡터와 문맥 벡터의 평균을 이용한다.
이를 통해 다음과 같이 단어의 유사도 비교가 가능하며 아래와 같이 'banana'와 유사한 상위 10개 단어의 경우 과일이 대다수인 것을 확인할 수 있다.

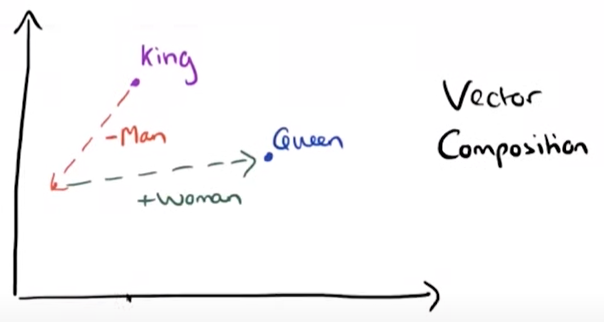
흥미로운 점은 아래와 같이 단어 벡터에 $-$를 취한다고 반의어가 등장하는 것은 아니지만,

단어들 간의 관계를 파악하는데 도움을 줄 수 있다

Reference)
Slide: https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1214/slides/cs224n-2021-lecture01-wordvecs1.pdf
Note: https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1214/readings/cs224n-2019-notes01-wordvecs1.pdf
Video: https://youtu.be/rmVRLeJRkl4
'교육 > CS224N winter 2021' 카테고리의 다른 글
| Lec 6) Simple and LSTM RNNs (0) | 2022.05.18 |
|---|---|
| Lec5) Language Models and RNNs (0) | 2022.05.11 |
| Lec 4) Dependency Parsing (0) | 2022.04.29 |
| Lec3) Backprop and Neural Networks (0) | 2022.04.22 |
| Lec2) Neural Classifiers (0) | 2022.04.11 |



