이전 강의: https://enjoythehobby.tistory.com/entry/Lec-2-Neural-Classifiers
Lec2) Neural Classifiers
이전 강의: https://enjoythehobby.tistory.com/entry/Lec1-Word-Vectors Lec1) Word Vectors Denotational semantics(표시적 의미론) ○ 텍스트를 분석을 위해 단어의 뜻을 어떻게 표현(represent)할 것인가? si..
enjoythehobby.tistory.com
NLP 대표 작업: 개체명 인식(Named entity recognition, NER)
글에서 단어를 찾아서 분류하는 작업 (사람, 장소, 날짜)
Last night, Paris Hilton wowed in a sequin gown.
Samuel Quinn was arrested in the Hilton Hotel in Paris in April 1989.
Paris와 Hilton은 중의적으로 사용되었으므로 모델이 단어를 문맥적으로 파악하는 능력이 필요하다.
○ 단순 개체명 인식(Simple NER)
개념: 각 단어의 문맥 윈도우 내에서의 분류
로지스틱(logistic) 분류기를 이용하여 윈도우 내의 단어 벡터들의 연결(concatenation)에 기반하여 중심 단어를 분류(yes, no)하는 것을 학습한다. 주로 multi-class softmax 함수를 사용한다.
예) "Paris"의 문맥 윈도우 2 조건으로 문장에서의 분류
the museums in Paris are amazing to see .
$$X_{window} = [ X_{museums} \: X_{in} \: X_{Paris} \: X_{are} \: X_{amazing}]^{T}$$
$X_{window}$는 5d 차원의 열벡터이다.
모든 단어의 분류를 위해서는 분류기를 문장의 각 단어가 중심 단어일 때의 벡터를 각각의 class에 대해 실행하면 된다.

확률적 경사하강법(Stochatic Gradient Descent, SGD)을 이용하여 위 모델의 파라미터를 업데이트한다.
$$\theta^{new}=\theta^{old}-\alpha\bigtriangledown_{\theta}J(\theta)$$
여기서 $\alpha$는 step size 또는 학습률(learning rate)이라고 한다
즉, 위 식과 같이 매개 변수에 손실 함수의 미분값을 일정량 빼주는 것으로 데이터 표현(단어 벡터)을 업데이트할 수 있다.
미분값 계산
○기울기, Gradients
함수 $f(x) =x^{3}$의 기울기는 $\frac{df}{dx}=3x^{2}$이고 미분값이 된다.
이 미분값은 해당 포인트에서 매개 변수 값을 조금 변화시켰을 경우 종속 변수가 얼만큼 변화할지 알려준다.
- $x=1$에서 기울기는 $3$이고 $0.01$ 변화시키면 변화량의 $3$배인 $1.01^{3}=1.03$이 된다.
- $x=4$에서 기울기는 $48$이고 $0.01$ 변화시키면 변화량의 $48$배인 $4.01^{3}=64.48$이 된다.
매개 변수가 많은 함수의 경우
$$f(x)=f(x_{1},x_{2},\cdots,x_{n})$$
각 매개 변수의 편미분 값으로 기울기가 정해진다
$$\frac{\partial f}{\partial x}=[\frac{\partial f}{\partial x_{1}},\frac{\partial f}{\partial x_{2}}, \cdots, \frac{\partial f}{\partial x_{n}}]$$
종속 변수까지 많은 함수의 경우
$$f(x)=[f_{1}(x_{1},x_{2},\cdots,x_{n}), \cdots, f_{m}(x_{1},x_{2},\cdots,x_{n})]$$
해당 함수의 $x$에 대한 편미분은 $m,n$ 행렬로 나타나며 이를 야코비(Jacobian) 행렬이라고 한다.
$$\frac{\partial{f}}{\partial{x}}= \begin{bmatrix}
\frac{\partial{f_{1}}}{\partial{x_{1}}} & \cdots & \frac{\partial{f_{1}}}{\partial{x_{n}}} \\
\vdots & \ddots & \vdots \\
\frac{\partial{f_{m}}}{\partial{x_{1}}} & \cdots & \frac{\partial{f_{m}}}{\partial{x_{n}}} \\
\end{bmatrix}$$
○ 연쇄 법칙(Chain rule)
$z=3y$, $y=x^{2}$일 때 $z$를 $x$에 대해 미분하면, 아래와 같다.
$$\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}=3\times2x=6x$$
위 방식을 여러 변수에 대해 적용하면, 야코비(Jacobian) 행렬의 곱으로 표현할 수 있다.
$$h=f(z)$$
$$z=Wx+b$$
$$\frac{\partial{h}}{\partial{x}}=\frac{\partial{h}}{\partial{z}}\frac{\partial{z}}{\partial{x}}=\cdots$$
예시 1) $h=f(z), \: h,z\in \mathbb{R}^{n}$일 때, $\frac{\partial{h}}{\partial{z}}?$
$h_{i}=f(z_{i})$ 각, 하나의 변수 $i$에 대해서 야코비는 다음과 같이 정의된다
$$(\frac{\partial{h}}{\partial{z}})_{ij}=\frac{\partial{h_{i}}}{\partial{z}_{j}}=\frac{\partial}{\partial{z}_{j}}f(z_{i})$$
$$=\left\{\begin{matrix}
f'(z_{i}) \quad \texttt{if} \; i=j \\ 0 \quad \texttt{if} \; \texttt{otherwise}
\end{matrix}\right.$$
$$\therefore\frac{\partial{h}}{\partial{z}}= \begin{bmatrix}
f'(z_{1}) & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & f'(z_{n}) \\
\end{bmatrix}=diag(f'(z))$$
예시 2) 다른 야코비(Jacobian) 행렬들
$$\frac{\partial}{\partial{x}}(Wx+b)=W$$
$$\frac{\partial}{\partial{b}}(Wx+b)=I,\; \texttt{항등행렬(Identity matrix)}$$
$$\frac{\partial}{\partial{u}}(u^{T}h)=h^{T}$$
○ 신경망의 야코비(Jacobian) 행렬 구하기

다시 개채명 인식 신경망으로 돌아와서 각각의 매개 변수($W$, $b$)에 대해 미분 값을 구해보자
1. $\frac{\partial{s}}{\partial{b}}$의 경우
우선, $h$의 경우 합성 함수 형태이므로 아래와 같이 두 개의 식으로 나눌 수 있다.
$$h=f(Wx+b)=f(z), \quad z=Wx+b$$
$b$에 대한 미분 역시 식(1)과 같이 연쇄 법칙을 이용하여 표현할 수 있다.
$$\frac{\partial{s}}{\partial{b}} = \frac{\partial{s}}{\partial{h}}\frac{\partial{h}}{\partial{z}}\frac{\partial{z}}{\partial{b}} \tag{1}$$
각각의 야코비 행렬은 다음과 같이 정리된다.
$$\frac{\partial{s}}{\partial{h}}=\frac{\partial}{\partial{h}}(u^{T}h)=u^{T} \tag{2}$$
$$\frac{\partial{h}}{\partial{z}}=\frac{\partial{f(z)}}{\partial{z}}=diag(f'(z)) \tag{3}$$
$$\frac{\partial{z}}{\partial{b}}=\frac{\partial{}}{\partial{b}}(Wx+b)=I \tag{4}$$
즉 식(2), (3), (4)를 전부 식(1)에 대입하면,
$$\therefore \frac{\partial{s}}{\partial{b}} = u^{T} \ast diag(f'(z))$$
여기서 $\ast$는 행렬 요소의 곱을 의미한다
2. $\frac{\partial{s}}{\partial{W}}$의 경우
식 (1)에서 $\frac{\partial{z}}{\partial{b}}$를 $\frac{\partial{z}}{\partial{W}}$로만 바꾸어서 생각하면 된다.
$$\frac{\partial{s}}{\partial{W}} = \frac{\partial{s}}{\partial{h}}\frac{\partial{h}}{\partial{z}}\frac{\partial{z}}{\partial{W}} = \textcolor{blue}{\delta}\frac{\partial{z}}{\partial{W}} \tag{5}$$
즉, 겹치는 부분을 $\textcolor{blue}{\delta}$로 표현하면,
$$ \frac{\partial{s}}{\partial{b}} = \textcolor{blue}{\delta}\frac{\partial{z}}{\partial{b}}= \textcolor{blue}{\delta}$$
$$\textcolor{blue}{\delta=\frac{\partial{s}}{\partial{h}}\frac{\partial{h}}{\partial{z}}= u^{T} \ast diag(f'(z))}$$
이며, $\textcolor{blue}{\delta}$는 'local error signal'이라고 한다.
여기서 $\frac{\partial{s}}{\partial{W}}$는 $W\in \mathbb{R}^{n\times m}$이므로
n,m 입력값과 1 출력값을 가지며, gradient는 1,n,m의 차원을 가진다.
$$\theta^{new}=\theta^{old}-\alpha\bigtriangledown_{\theta}J(\theta)$$
SGD를 통해 변수 업데이트를 편하게 하기 위해서 차원변환을 통해 graient의 차원을 n,m으로 만들어주면 변수와 같아지므로 편하게 계산할 수 있다.
$$\frac{\partial{s}}{\partial{W}}= \begin{bmatrix}
\frac{\partial{s}}{\partial{W_{11}}} & \cdots & \frac{\partial{s}}{\partial{W_{1m}}} \\
\vdots & \ddots & \vdots \\
\frac{\partial{s}}{\partial{W_{n1}}} & \cdots & \frac{\partial{s}}{\partial{W_{nm}}} \\
\end{bmatrix}$$
결국 식(5)에서 $z=Wx+b$이므로
$$\frac{\partial{s}}{\partial{W}}=\delta^{T}x^{T}$$
가 되며 $x$는 'local input signal' $\delta$는 $z$에서의 'local error signal'이다.

왜 전치 시키는가?
$$\frac{\partial{s}}{\partial{W}}_{nm}=\delta^{T}_{n}x^{T}_{m}$$
$$=\begin{bmatrix}
\delta_{1} \\
\vdots \\
\delta_{n} \\
\end{bmatrix}
\begin{bmatrix}
x_{1} & \cdots & x_{m} \\
\end{bmatrix}=
\begin{bmatrix}
\delta_{1}x_{1} & \cdots & \delta_{1}x_{m} \\
\vdots & \ddots & \vdots \\
\delta_{n}x_{1} & \cdots & \delta_{n}x_{m} \\
\end{bmatrix}$$
Hacky answer: this makes the dimensions work out!
유사하게, $\frac{\partial{s}}{\partial{b}} = u^{T} \ast diag(f'(z))$는 행 벡터이다.
그러나 $b$가 열 벡터 이므로 마지막에 차원 변환을 해주어야 한다.
야코비 변환과 차원 변환을 이용하여 SGD와 연쇄법칙을 손쉽게 계산할 수 있다.
그 외에 매번 차원에 맞추어서 차원 변환을 해주는 방법이 있을 수 있다.
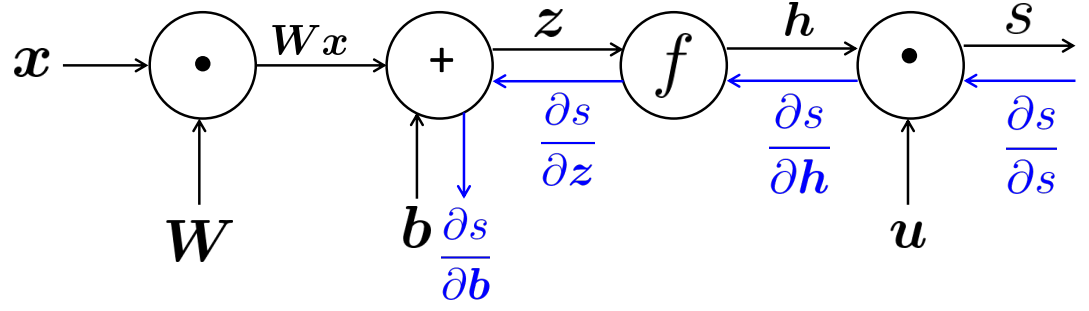
○ 순전파 (Forward propagation)
그래프를 통해 신경망에서의 연산이 순서대로 어떻게 흘러가는지 확인이 가능하다. 순전파란 feedfoward라고도 하며, 입력에서 출력 방향으로 이동하면서 연산을 수행하는 것을 말한다.

○ 역전파 (Back propagation)
역전파의 경우 출력으로부터 반대로 입력층 방향으로 gradient를 계산하며 변수를 업데이트 해 나갑니다.
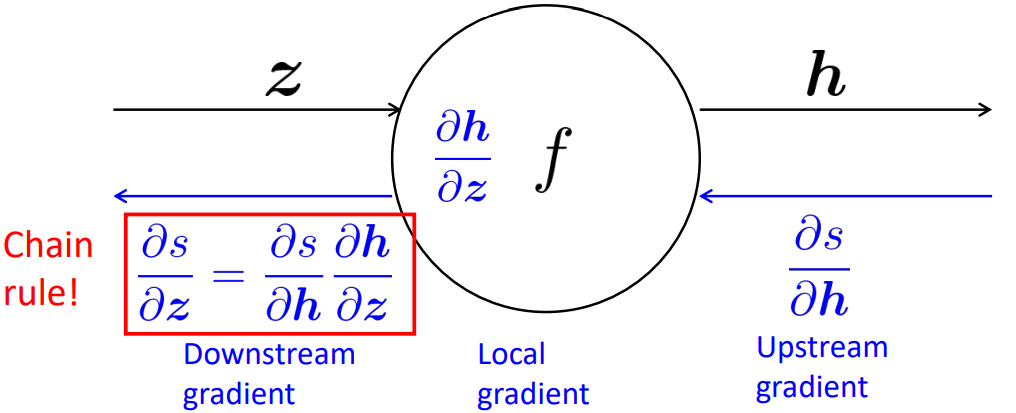
단일 노드를 확대해서 보면 각각의 노드에는 local gradient가 존재하며, 이를 출력단에서 들어오는 Upstream gradient와 연산하면 연쇄법칙에 의해 또 간단한 형태의 gradient로 표현된다.
즉 [Downstream gradient] = [Upstream gradient] × [Local gradient]
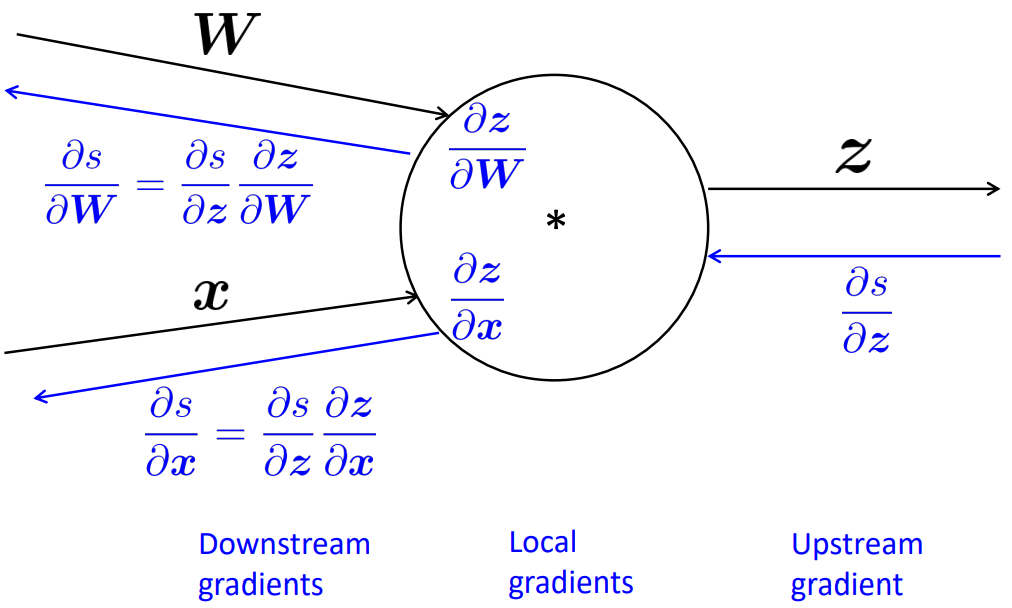
이는 입력이 여러 개인 노드에 대해서도 동일하게 적용한다.
출력이 여러 개인 노드의 경우에는 각각의 upstream gradient의 합으로 downstream gradient를 구하면 된다.

역전파를 통해 매개 변수를 update하면 중복되는 계산을 한 번에 수행하여 효율적인 계산이 가능하다
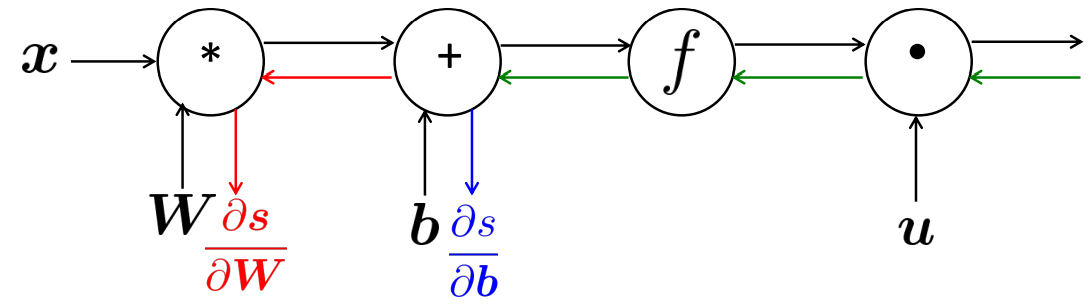
결과적으로 각 노드에 대한 연산은 한번만 수행해주면 되므로 순전파와 역전파의 복잡도는 같다.
○ 수치적(Numerical) Gradient
작은 변화량 $h$(약 1e-4)을 이용하여 수치적으로 gradient를 구할 수 있다.
$$f'(x)\approx \frac{f(x+h)-f(x-h))}{2h}$$
쉽고 정확하게 적용할 수 있지만, 근사적으로 굉장히 느리다. 따라서 일반적으로 분석적(analytic)으로 구한 값이 정확한지 비교용으로 사용된다.
Reference)
Slide: cs224n-2021-lecture03-neuralnets.pdf (stanford.edu)
Note: CS224n: Natural Language Processing with Deep Learning Lecture Notes: Part III Neural Networks, Backpropagation (stanford.edu)
Video: https://youtu.be/X0Jw4kgaFlg?list=PLoROMvodv4rOSH4v6133s9LFPRHjEmbmJ
'교육 > CS224N winter 2021' 카테고리의 다른 글
| Lec 6) Simple and LSTM RNNs (0) | 2022.05.18 |
|---|---|
| Lec5) Language Models and RNNs (0) | 2022.05.11 |
| Lec 4) Dependency Parsing (0) | 2022.04.29 |
| Lec2) Neural Classifiers (0) | 2022.04.11 |
| Lec1) Word Vectors (0) | 2022.04.11 |



